题目内容
8.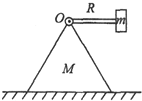 如图所示为打夯机的结构示意图,质量为m的重锤可绕转轴O转动,其转动半径为R,打夯机底座的质量为M,重锤和转轴O之间的连接杆质量可以忽略不计,重力加速度为g,不计转轴的摩擦以及空气阻力影响.将重锤从水平位置无初速地自由释放后,底座保持静止,试求:
如图所示为打夯机的结构示意图,质量为m的重锤可绕转轴O转动,其转动半径为R,打夯机底座的质量为M,重锤和转轴O之间的连接杆质量可以忽略不计,重力加速度为g,不计转轴的摩擦以及空气阻力影响.将重锤从水平位置无初速地自由释放后,底座保持静止,试求:(1)重锤运动到最低点时的速度为多大?
(2)重锤运动到最低点时,底座对地面的压力为多大?
分析 (1)对重锤,从水平位置运动到最低点的过程中,根据动能定理列式即可求解;
(2)在最低点,分别对重锤和底座受力分析,根据牛顿第二定律结合平衡条件列式求解.
解答 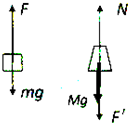 解:(1)对重锤,从水平位置运动到最低点的过程中,根据动能定理得:
解:(1)对重锤,从水平位置运动到最低点的过程中,根据动能定理得:
mgR=$\frac{1}{2}m{v}^{2}$
解得:$v=\sqrt{2gR}$
(2)在最低点,分别对重锤和底座受力分析,如图所示,设轻杆对重锤弹力为F,轻杆对底座弹力为F′,地面对底座的弹力为N,底座对地面的弹力为N′,
对重锤有:F-mg=m$\frac{{v}^{2}}{R}$,对底座有:F′+Mg=N,
由牛顿第三定律和平衡条件得:N=N′,F′=F,联立解得:N′=3mg+Mg
答:(1)重锤运动到最低点时的速度为$\sqrt{2gR}$;
(2)重锤运动到最低点时,底座对地面的压力为3mg+Mg.
点评 解决本题的关键采用隔离法分析,对重锤,在竖直方向上的合力提供圆周运动的向心力.对打夯机受力平衡.

练习册系列答案
相关题目
18.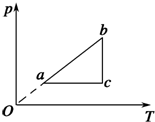 一定量的理想气体从状态a开始,经历三个过程ab、bc、ca回到原状态,其pT图象如图所示.下列判断正确的是( )
一定量的理想气体从状态a开始,经历三个过程ab、bc、ca回到原状态,其pT图象如图所示.下列判断正确的是( )
 一定量的理想气体从状态a开始,经历三个过程ab、bc、ca回到原状态,其pT图象如图所示.下列判断正确的是( )
一定量的理想气体从状态a开始,经历三个过程ab、bc、ca回到原状态,其pT图象如图所示.下列判断正确的是( )| A. | 过程ab中气体一定吸热 | |
| B. | a和c两个状态中,容器壁单位面积、单位时间内受到气体分子撞击的次数不同 | |
| C. | 过程ca中外界对气体所做的功等于气体所放的热 | |
| D. | a、b和c三个状态中,状态a分子的平均动能最小 |
16.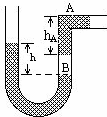 如图所示,U形管两臂竖直固定,右管中一段水银柱A与管底部水银间有一段空气柱B被封于右臂管子的中部,A有部分水银在水平管中,设U形管内粗细均匀,两端均开口与大气相通.现保持温度不变,向左管缓慢注入少量水银,则重新平衡后( )
如图所示,U形管两臂竖直固定,右管中一段水银柱A与管底部水银间有一段空气柱B被封于右臂管子的中部,A有部分水银在水平管中,设U形管内粗细均匀,两端均开口与大气相通.现保持温度不变,向左管缓慢注入少量水银,则重新平衡后( )
 如图所示,U形管两臂竖直固定,右管中一段水银柱A与管底部水银间有一段空气柱B被封于右臂管子的中部,A有部分水银在水平管中,设U形管内粗细均匀,两端均开口与大气相通.现保持温度不变,向左管缓慢注入少量水银,则重新平衡后( )
如图所示,U形管两臂竖直固定,右管中一段水银柱A与管底部水银间有一段空气柱B被封于右臂管子的中部,A有部分水银在水平管中,设U形管内粗细均匀,两端均开口与大气相通.现保持温度不变,向左管缓慢注入少量水银,则重新平衡后( )| A. | 图中h减小 | B. | 空气柱B的长度不变 | ||
| C. | 空气柱B的压强增大 | D. | 图中h不变 |
20.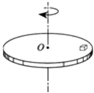 一个质量为M的物体在水平转盘上.距离转轴的距离为r,当转盘的转速为n时,物体相对于转盘静止,如果转盘的转速增大时,物体仍然相对于转盘静止.则下列说法中正确的是( )
一个质量为M的物体在水平转盘上.距离转轴的距离为r,当转盘的转速为n时,物体相对于转盘静止,如果转盘的转速增大时,物体仍然相对于转盘静止.则下列说法中正确的是( )
 一个质量为M的物体在水平转盘上.距离转轴的距离为r,当转盘的转速为n时,物体相对于转盘静止,如果转盘的转速增大时,物体仍然相对于转盘静止.则下列说法中正确的是( )
一个质量为M的物体在水平转盘上.距离转轴的距离为r,当转盘的转速为n时,物体相对于转盘静止,如果转盘的转速增大时,物体仍然相对于转盘静止.则下列说法中正确的是( )| A. | 物体受到的支持力变大 | B. | 物体受到的静摩擦力增大 | ||
| C. | 物体受到的合外力不变 | D. | 物体对转盘的压力不变 |
18.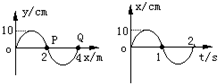 如图所示,为一简谐横波在t=1s时的波形图和该波上一质点P的振动图象,根据图象可知,下列说法正确的是( )
如图所示,为一简谐横波在t=1s时的波形图和该波上一质点P的振动图象,根据图象可知,下列说法正确的是( )
 如图所示,为一简谐横波在t=1s时的波形图和该波上一质点P的振动图象,根据图象可知,下列说法正确的是( )
如图所示,为一简谐横波在t=1s时的波形图和该波上一质点P的振动图象,根据图象可知,下列说法正确的是( )| A. | Q点速度向y轴负方向 | B. | P点振幅为5cm | ||
| C. | 波沿x轴正方向传播,v=10m/s | D. | 波沿x轴负方向传播,v=2m/s |
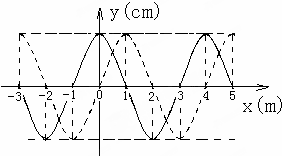 如图所示,实线是某时刻的波形图,虚线是0.2s后的波形图.若波向左传播,求:
如图所示,实线是某时刻的波形图,虚线是0.2s后的波形图.若波向左传播,求: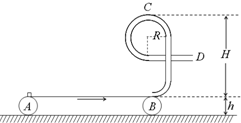 如图所示,水平传送带AB的右端与在竖直面内的用内径光滑的钢管弯成的“9”形固定轨道相接,钢管内径很小.传送带的运行速度v0=4.0m/s,将质量m=1kg的可看做质点的滑块无初速地放在传送带的A端.已知传送带长度L=4.0m,离地高度h=0.4m,“9”字全髙H=0.6m,“9”字上半部分$\frac{3}{4}$圆弧的半径R=0.1m,滑块与传送带间的动摩擦因数μ=0.2,重力加速度g=10m/s2,试求:
如图所示,水平传送带AB的右端与在竖直面内的用内径光滑的钢管弯成的“9”形固定轨道相接,钢管内径很小.传送带的运行速度v0=4.0m/s,将质量m=1kg的可看做质点的滑块无初速地放在传送带的A端.已知传送带长度L=4.0m,离地高度h=0.4m,“9”字全髙H=0.6m,“9”字上半部分$\frac{3}{4}$圆弧的半径R=0.1m,滑块与传送带间的动摩擦因数μ=0.2,重力加速度g=10m/s2,试求:
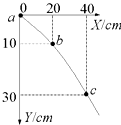 某同学在做《研究平抛物体的运动》实验得到图示运动轨迹,a、b、c三点的位置坐标已经在图上已经标出
某同学在做《研究平抛物体的运动》实验得到图示运动轨迹,a、b、c三点的位置坐标已经在图上已经标出