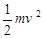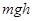题目内容
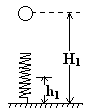
如图所示,AB为一长为l并以速度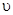 顺时针匀速转动的传送带,BCD部分为一半径为r、竖直放置的粗糙半圆形轨道,直径BD恰好竖直,并与传送带相切于B点。现将一质量为m的小滑块无初速地放在传送带的左端A点上,已知滑块与传送带间的动摩擦因数为
顺时针匀速转动的传送带,BCD部分为一半径为r、竖直放置的粗糙半圆形轨道,直径BD恰好竖直,并与传送带相切于B点。现将一质量为m的小滑块无初速地放在传送带的左端A点上,已知滑块与传送带间的动摩擦因数为 >
>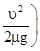 。求:
。求:
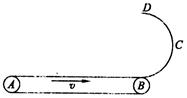
(1)滑块到达B点时对轨道的压力大小;
(2)滑块恰好能到达D点,求滑块在粗糙半圆形轨道中克服摩擦力的功;
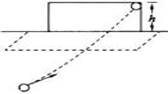
(3)滑块从D熙 再次掉到传送带上E点,求AE的距离。
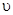 顺时针匀速转动的传送带,BCD部分为一半径为r、竖直放置的粗糙半圆形轨道,直径BD恰好竖直,并与传送带相切于B点。现将一质量为m的小滑块无初速地放在传送带的左端A点上,已知滑块与传送带间的动摩擦因数为
顺时针匀速转动的传送带,BCD部分为一半径为r、竖直放置的粗糙半圆形轨道,直径BD恰好竖直,并与传送带相切于B点。现将一质量为m的小滑块无初速地放在传送带的左端A点上,已知滑块与传送带间的动摩擦因数为 >
>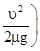 。求:
。求:
(1)滑块到达B点时对轨道的压力大小;
(2)滑块恰好能到达D点,求滑块在粗糙半圆形轨道中克服摩擦力的功;
(3)滑块从D熙 再次掉到传送带上E点,求AE的距离。
(1)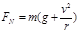 (2)
(2)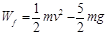 (3)
(3)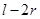
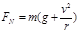 (2)
(2)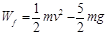 (3)
(3)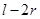
(1)设滑块在摩擦力作用下从A到B一直被加速,且设刚好到达B点前的速度为v,
则: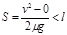 1(2分)
1(2分)
故滑块在传送带上是先加速后匀速,到达B点时的速度为v
由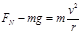 2(2分)
2(2分)
得: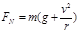 。 3(1分)
。 3(1分)
(2)滑块恰好能到达D点,则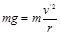 。 4(2分)
。 4(2分)
由动能定理得: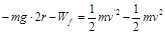 , 5(2分)
, 5(2分)
得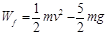 。 6(1分)
。 6(1分)
(3)滑块从D点再次掉到传送带上E点做平抛运动,即
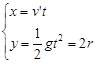 , 7(2分)
, 7(2分)
得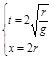 , 8(2分)
, 8(2分)
故AE的距离为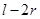 。 9(2分)
。 9(2分)
则:
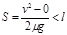 1(2分)
1(2分)故滑块在传送带上是先加速后匀速,到达B点时的速度为v
由
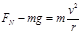 2(2分)
2(2分)得:
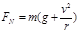 。 3(1分)
。 3(1分)(2)滑块恰好能到达D点,则
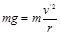 。 4(2分)
。 4(2分)由动能定理得:
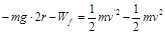 , 5(2分)
, 5(2分)得
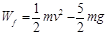 。 6(1分)
。 6(1分)(3)滑块从D点再次掉到传送带上E点做平抛运动,即
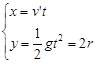 , 7(2分)
, 7(2分)得
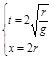 , 8(2分)
, 8(2分)故AE的距离为
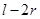 。 9(2分)
。 9(2分)
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目