题目内容
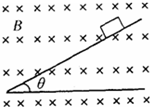质量为m、带电量为q的小物块，从倾角为θ的光滑绝缘斜面上由静止下滑，整个斜面置于方向水平向里的匀强磁场中，磁感应强度为B，如图所示．若带电小物块下滑后某时刻会离开斜面，则下面说法中正确的是（ ）分析：由于小物块下滑后某时刻会离开斜面，故其所受洛伦兹力应该垂直斜面向上，根据左手定则可知小物块可判定其所带电性；小物块在斜面上运动时其加速度由重力沿斜面方向的分力提供，根据牛顿第二定律可以求出物体的加速度，从而判定物体是否是匀加速运动；小物块离开斜面时垂直斜面方向合力为0；
解答：解：A、由于小物块下滑后某时刻会离开斜面，故其所受洛伦兹力应该垂直斜面向上，根据左手定则可知小物块一定带有负电荷，故A错误；
B、小物块在斜面上运动时其加速度由重力沿斜面方向的分力提供，故有mgsinθ=ma，故a=gsinθ，所以小物块在斜面上运动时做匀加速直线运动，故B正确；
C、由以上分析可知，C错误；
D、小物块离开斜面时有qvB=mgcosθ，解得此时小物块的速率v=
，故D正确．
故选BD．
B、小物块在斜面上运动时其加速度由重力沿斜面方向的分力提供，故有mgsinθ=ma，故a=gsinθ，所以小物块在斜面上运动时做匀加速直线运动，故B正确；
C、由以上分析可知，C错误；
D、小物块离开斜面时有qvB=mgcosθ，解得此时小物块的速率v=
| mgcosθ |
| qB |
故选BD．
点评：本题考查了左手定则，受力分析，牛顿第二定律，难度不大，代表性较强．
练习册系列答案
相关题目
如图所示，两个相同的带等量正电的圆环正对放置，电荷均匀分布．O1O2为两圆心的连线，P为O1O2的中点．一质量为m、带电量为-q的点电荷以初速度v0从O1点沿O1O2方向射出，恰能到达P点．不计重力，则点电荷-q克服电场力做的功为
（2010?苏州二模）如图所示，K1、K2闭合时，一质量为m、带电量为q的液滴，静止在电容器的A、B两平行金属板间．现保持K1闭合，将K2断开，然后将B板向下平移一段距离，则下列说法正确的是（ ）
（2006?盐城模拟）如图所示，在直角坐系中的第Ⅰ象限中存在沿y轴负方向的匀强电场，在第Ⅳ象限中存在垂直纸面的匀强磁场，一质量为m、带电量为q的粒子（不计重力）在y轴上的A（0，3）以平行x轴的初速度v0=120m/s射人电场区，然后从电场区进入磁场区，又从磁场区进入电场区，并通过x轴上P点（4.5，0）和Q点（8，0）各一次．已知该粒子的荷质比为
的直线．磁场方向垂直纸面向外．一质量为m、带电量为q的正粒子从y轴上P点以初速度v0垂直y轴射入匀强电场，在电场力作用下从x轴上Q点以与x轴正方向45°角进入匀强磁场．已知OQ＝l，不计粒子重力．求：
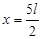的直线．磁场方向垂直纸面向外．一质量为m、带电量为q的正粒子从y轴上P点以初速度v0垂直y轴射入匀强电场，在电场力作用下从x轴上Q点以与x轴正方向45°角进入匀强磁场．已知OQ＝l，不计粒子重力．求：