题目内容
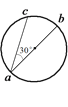
【题目】如图所示，ab是半径为R的圆的一条直径，该圆处于匀强电场中，场强大小为E，方向一定。在圆周平面内，将一带正电q的小球从a点以相同的动能抛出，抛出方向不同时，小球会经过圆周上不同的点，在这些所有的点中，到达c点时小球的动能最大。已知∠cab=30°，若不计重力和空气阻力，试求：
（1）电场方向与ac间的夹角θ为多大。
（2）若小球在a点时初速度方向与电场方向垂直，则小球恰好落在c点，那么初动能为多大。
【答案】（1）电场方向与ac夹角30°，（2）初动能为
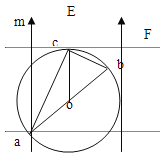
【解析】(1)小球在c点时的动能最大，即c点的电势最低．作过c点与圆周相切的线，切线为等势线，Oc方向即为电场方向，其与直径ac夹角为：θ＝∠acO＝30°
(2)小球做类平抛运动．有：ad＝v0t ①
在沿着电场线方向有： 
②
由图几何关系可得： 
③
＝
·sinθ＝
④
＝·cosθ+R＝3R∕2⑤
将③、④、⑤式代入①、②两式
并解得
．所以
练习册系列答案
轻松课堂单元测试AB卷系列答案
小题狂做系列答案
相关题目
