题目内容
9. 很多企业单位的大门都装有自动栏杆,某大门的自动栏杆简易图如图所示,立柱从地面G到转轴O点高H=0.8m,栏杆从转轴O到末端P长L=6m,平时无车辆进出,栏杆置于水平位置,左边有门卫室,AB为竖直墙,高h=2m,BC为房屋宽,宽度b=6m,倾斜屋顶成45°,顶点为E.某天下雨,有水滴粘在栏杆上,当启动自动栏杆逆时针匀角速转到竖直位置,栏杆突然停止,而粘在栏杆上的水滴由于惯性以栏杆停止前的瞬间速度水平飞出,发现从P点飞出的水滴恰好沿EC经过E点.(不计空气阻力,g=10m/s2)求:
很多企业单位的大门都装有自动栏杆,某大门的自动栏杆简易图如图所示,立柱从地面G到转轴O点高H=0.8m,栏杆从转轴O到末端P长L=6m,平时无车辆进出,栏杆置于水平位置,左边有门卫室,AB为竖直墙,高h=2m,BC为房屋宽,宽度b=6m,倾斜屋顶成45°,顶点为E.某天下雨,有水滴粘在栏杆上,当启动自动栏杆逆时针匀角速转到竖直位置,栏杆突然停止,而粘在栏杆上的水滴由于惯性以栏杆停止前的瞬间速度水平飞出,发现从P点飞出的水滴恰好沿EC经过E点.(不计空气阻力,g=10m/s2)求:(1)栏杆转动的角速度的大小.
(2)竖直墙AB与立柱GO之间的水平距离s.
(3)通过计算说明,栏杆上距离O点为l=2m的Q点处的水滴是否能落在倾斜屋顶BE上.
分析 (1、2)P处水滴做平抛运动,由平抛运动规律及圆周运动线速度和角速度关系联立可求得角速度及竖直墙AB与立柱GO之间的水平距离s.
(3)同理由平抛运动的规律及圆周运动知识可分析判断能否落到屋顶.
解答 解:(1)P处水滴做平抛运动,时间为t1,P处与E点所在水平面的高度差为h1;则有:
h1=H+L-h-3=0.8+6-2-3=1.8m;
竖直方向有:vy=$\sqrt{2g{h}_{1}}$
下落高度h1=$\frac{1}{2}$gt12
水平位移:s+3=vPt1
由圆周运动规律可得:
vP=ωL
而vP=vy
联立解得:ω=1rad/s
s=0.6m;
(3)假设Q处水滴落到BC所在平面的高度差为h2,时间为t2,水平位移为x,则有:
h2=H+l-h=0.8m;
vQ=ωl
h2=$\frac{1}{2}$gt22
x=vQt2
解得:x=0.8m;
x>s;
故一定可以落到屋顶上;
答::(1)栏杆转动的角速度的大小为1rad/s
(2)竖直墙AB与立柱GO之间的水平距离s为0.6m;
(3)通过计算说明,栏杆上距离O点为l=2m的Q点处的水滴能落在倾斜屋顶BE上.
点评 本题考查平抛运动及圆周运动规律,要注意平抛运动在水平方向为匀速直线运动,竖直方向做自由落体运动.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
4.下列有关物理学史或物理现象的说法中正确的是( )
| A. | 停在高压线上的小鸟没有被电击,是因为小鸟所停处电势为零 | |
| B. | 法拉第以他深刻的洞察力提出场的概念,并引入了电场线 | |
| C. | 安培通过实验研究,发现了电流周围存在磁场,并通过安培定则判断磁场方向 | |
| D. | 超高压带电作业的工人所穿工作服的织物中不能掺入金属丝 |
1. 科学探究活动通常包括以下环节:提出问题,作出假设,制定计划,搜集证据,评估交流等.一组同学研究“运动物体所受空气阻力与运动速度关系”的探究过程如下
科学探究活动通常包括以下环节:提出问题,作出假设,制定计划,搜集证据,评估交流等.一组同学研究“运动物体所受空气阻力与运动速度关系”的探究过程如下
A.有同学认为:运动物体所受空气阻力可能与其运动速度有关
B.他们计划利用一些“小纸杯”作为研究对象,用超声测距仪等仪器测量“小纸杯”在空中直线下落时的下落距离、速度随时间变化的规律,以验证假设
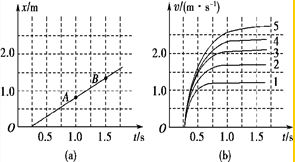
C.在相同的实验条件下,同学们首先测量了单只“小纸杯”在空中下落过程中不同时刻的下落距离,将数据填入表中,如图(a)是对应的位移-时间图线.然后将不同数量的“小纸杯”叠放在一起从空中下落,分别测出它们的速度-时间图线,如图(b)中图线1、2、3、4、5所示
D.同学们对实验数据进行分析、归纳后,证实了他们的假设.
回答下列提问:
(1)与上述过程中A、C步骤相应的科学探究环节分别是作出假设、搜集证据;
(2)图(a)中的AB段反映了运动物体在做匀速直线运动,表中x处的值为1.937;
(3)图(b)中各条图线具有共同特点,“小纸杯”在下落的开始阶段做加速度逐渐减小的加速运动,最后“小纸杯”做匀速运动;
 科学探究活动通常包括以下环节:提出问题,作出假设,制定计划,搜集证据,评估交流等.一组同学研究“运动物体所受空气阻力与运动速度关系”的探究过程如下
科学探究活动通常包括以下环节:提出问题,作出假设,制定计划,搜集证据,评估交流等.一组同学研究“运动物体所受空气阻力与运动速度关系”的探究过程如下A.有同学认为:运动物体所受空气阻力可能与其运动速度有关
B.他们计划利用一些“小纸杯”作为研究对象,用超声测距仪等仪器测量“小纸杯”在空中直线下落时的下落距离、速度随时间变化的规律,以验证假设
C.在相同的实验条件下,同学们首先测量了单只“小纸杯”在空中下落过程中不同时刻的下落距离,将数据填入表中,如图(a)是对应的位移-时间图线.然后将不同数量的“小纸杯”叠放在一起从空中下落,分别测出它们的速度-时间图线,如图(b)中图线1、2、3、4、5所示
D.同学们对实验数据进行分析、归纳后,证实了他们的假设.
回答下列提问:
(1)与上述过程中A、C步骤相应的科学探究环节分别是作出假设、搜集证据;
(2)图(a)中的AB段反映了运动物体在做匀速直线运动,表中x处的值为1.937;
(3)图(b)中各条图线具有共同特点,“小纸杯”在下落的开始阶段做加速度逐渐减小的加速运动,最后“小纸杯”做匀速运动;
| 时间(s) | 下落距离(m) |
| 0.0 | 0.000 |
| 0.4 | 0.036 |
| 0.8 | 0.469 |
| 1.2 | 0.957 |
| 1.6 | 1.447 |
| 2.0 | x |
18.某同学在篮球场上锻炼身体,一次投篮时篮球恰好垂直打在篮板上,设篮球撞击篮板处与抛出点的竖直距离为x,水平距离为2x,篮球抛出时速度与地面的夹角为θ,大小为v,则下列判断正确的是( )
| A. | θ=30° | B. | θ=60° | C. | v=$\sqrt{2gx}$ | D. | v=2$\sqrt{gx}$ |
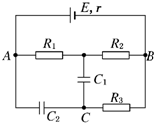 如图所示,电源电动势E=12V,内阻r=1Ω,电阻R1=3Ω,R2=2Ω,R3=5Ω,电容器的电容C1=4 μF,C2=1 μF,求C1、C2所带电荷量.
如图所示,电源电动势E=12V,内阻r=1Ω,电阻R1=3Ω,R2=2Ω,R3=5Ω,电容器的电容C1=4 μF,C2=1 μF,求C1、C2所带电荷量.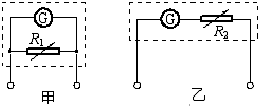 如图所示,将一个电流表G和另一个电阻连接可以改装成电压表或电流表,则甲图对应的是电流表(电压表或电流表),要使它的量程减小,应使R1增大.(填“增大”或“减小”).
如图所示,将一个电流表G和另一个电阻连接可以改装成电压表或电流表,则甲图对应的是电流表(电压表或电流表),要使它的量程减小,应使R1增大.(填“增大”或“减小”).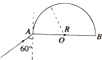 一底面半径为R的半圆柱形透明体的折射率为n=$\sqrt{3}$,横截面如图所示,O表示半圆柱形截面的圆心,一束极窄的光线在横截面内从AOB边上的A点以60°的入射角入射,已知真空中的光速为c.sin35°=$\frac{\sqrt{3}}{3}$,求该光线从A点进入透明体到从B点离开透明体所经历的时间.
一底面半径为R的半圆柱形透明体的折射率为n=$\sqrt{3}$,横截面如图所示,O表示半圆柱形截面的圆心,一束极窄的光线在横截面内从AOB边上的A点以60°的入射角入射,已知真空中的光速为c.sin35°=$\frac{\sqrt{3}}{3}$,求该光线从A点进入透明体到从B点离开透明体所经历的时间.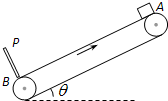 如图所示,长L=9m的传送带与水平面的倾角θ=37°,在电动机的带动下以v=4m/s的恒定速率沿顺时针方向运行,在传送带的B端有一离传送带很近的挡板P可将带上的物块挡住,在传送带的A端静止释放一质量m=1kg的物体,它与传送带间的动摩擦因数μ=0.5,物块与挡板的碰撞能量损失及碰撞时间不计(g=10m/s2,sin37°=0.6),求:
如图所示,长L=9m的传送带与水平面的倾角θ=37°,在电动机的带动下以v=4m/s的恒定速率沿顺时针方向运行,在传送带的B端有一离传送带很近的挡板P可将带上的物块挡住,在传送带的A端静止释放一质量m=1kg的物体,它与传送带间的动摩擦因数μ=0.5,物块与挡板的碰撞能量损失及碰撞时间不计(g=10m/s2,sin37°=0.6),求: 如图所示,从高为0.8m的粗糙斜面顶端A点处,由静止释放一质量为2kg的滑块.滑块到达底端B点时的速度大小为3m/s.求滑块从A到B的过程中克服阻力做的功.
如图所示,从高为0.8m的粗糙斜面顶端A点处,由静止释放一质量为2kg的滑块.滑块到达底端B点时的速度大小为3m/s.求滑块从A到B的过程中克服阻力做的功.