题目内容
18.某同学在篮球场上锻炼身体,一次投篮时篮球恰好垂直打在篮板上,设篮球撞击篮板处与抛出点的竖直距离为x,水平距离为2x,篮球抛出时速度与地面的夹角为θ,大小为v,则下列判断正确的是( )| A. | θ=30° | B. | θ=60° | C. | v=$\sqrt{2gx}$ | D. | v=2$\sqrt{gx}$ |
分析 篮球垂直打在篮板上,采用逆向思维,篮球做平抛运动,结合平抛运动的规律求出篮球抛出时的速度大小和方向.
解答 解:采用逆向思维,篮球做平抛运动,根据x=$\frac{1}{2}g{t}^{2}$得,t=$\sqrt{\frac{2x}{g}}$,则篮球撞在篮板上的速度${v}_{0}=\frac{2x}{t}=\sqrt{2gx}$,可知抛出时竖直分速度${v}_{y}=gt=\sqrt{2gx}$,
根据平行四边形定则知,篮球抛出时的速度v=$\sqrt{{{v}_{0}}^{2}+{{v}_{y}}^{2}}=2\sqrt{gx}$.故D正确,C错误.
抛出时速度与地面夹角的正切值$tanθ=\frac{{v}_{y}}{{v}_{0}}=1$,解得θ=45°.故A、B错误.
故选:D.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解,基础题.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
6.物体在恒力作用下不可能做的运动是( )
| A. | 直线运动 | B. | 曲线运动 | C. | 匀速圆周运动 | D. | 平抛运动 |
10.如图是在胶片上呈现的某单色光衍射的图样,下列关于该图样的说法正确的是 ( )

| A. | 该图样说明光具有波动性 | |
| B. | 没有光子落在暗条纹处 | |
| C. | 每个光子在胶片上的落点是可以确定的 | |
| D. | 大量光子在胶片上的落点是有规律的 | |
| E. | 改用电子做该实验也能得到明暗相间的衍射图样 |
7.在太阳系中,若火星轨道的半长轴为a,公转周期为T,则下列关系正确的是( )
| A. | a=kT | B. | a=kT2 | C. | a2=kT2 | D. | a3=kT2 |
 很多企业单位的大门都装有自动栏杆,某大门的自动栏杆简易图如图所示,立柱从地面G到转轴O点高H=0.8m,栏杆从转轴O到末端P长L=6m,平时无车辆进出,栏杆置于水平位置,左边有门卫室,AB为竖直墙,高h=2m,BC为房屋宽,宽度b=6m,倾斜屋顶成45°,顶点为E.某天下雨,有水滴粘在栏杆上,当启动自动栏杆逆时针匀角速转到竖直位置,栏杆突然停止,而粘在栏杆上的水滴由于惯性以栏杆停止前的瞬间速度水平飞出,发现从P点飞出的水滴恰好沿EC经过E点.(不计空气阻力,g=10m/s2)求:
很多企业单位的大门都装有自动栏杆,某大门的自动栏杆简易图如图所示,立柱从地面G到转轴O点高H=0.8m,栏杆从转轴O到末端P长L=6m,平时无车辆进出,栏杆置于水平位置,左边有门卫室,AB为竖直墙,高h=2m,BC为房屋宽,宽度b=6m,倾斜屋顶成45°,顶点为E.某天下雨,有水滴粘在栏杆上,当启动自动栏杆逆时针匀角速转到竖直位置,栏杆突然停止,而粘在栏杆上的水滴由于惯性以栏杆停止前的瞬间速度水平飞出,发现从P点飞出的水滴恰好沿EC经过E点.(不计空气阻力,g=10m/s2)求:
 利用如图所示的电路可以测量待测电源的电动势E和内电阻r,某实验小组在进行实验时先闭合开关S1、断开开关S2,测得电压表的示数为U1,然后闭合开关S2,测得电压表的示数为U2,过程中保持电阻箱的阻值始终为R,若将电压表视为理想电表,则根据测量的数据可得该电源的电动势为U1、内阻为$\frac{{U}_{1}-{U}_{2}}{{U}_{2}}R$.
利用如图所示的电路可以测量待测电源的电动势E和内电阻r,某实验小组在进行实验时先闭合开关S1、断开开关S2,测得电压表的示数为U1,然后闭合开关S2,测得电压表的示数为U2,过程中保持电阻箱的阻值始终为R,若将电压表视为理想电表,则根据测量的数据可得该电源的电动势为U1、内阻为$\frac{{U}_{1}-{U}_{2}}{{U}_{2}}R$.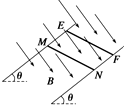 如图所示,相距为L的两条足够长的平行金属导轨,与水平面的夹角为θ,金属导轨电阻不计.导轨上有质量为m、电阻为R的两根相同的导体棒,导体棒MN上方轨道粗糙、导体棒MN所在位置及下方轨道光滑,整个空间存在垂直于导轨平面的匀强磁场,磁感应强度为B.将两根导体棒同时释放后,观察到导体棒MN下滑而EF保持静止,当MN下滑x距离后恰好达到最大速度时,EF与轨道间的摩擦力也刚好达到最大静摩擦力.求:
如图所示,相距为L的两条足够长的平行金属导轨,与水平面的夹角为θ,金属导轨电阻不计.导轨上有质量为m、电阻为R的两根相同的导体棒,导体棒MN上方轨道粗糙、导体棒MN所在位置及下方轨道光滑,整个空间存在垂直于导轨平面的匀强磁场,磁感应强度为B.将两根导体棒同时释放后,观察到导体棒MN下滑而EF保持静止,当MN下滑x距离后恰好达到最大速度时,EF与轨道间的摩擦力也刚好达到最大静摩擦力.求: