题目内容
空间存在水平向右的匀强电场,场强为50N/C一个带电小球的质量20g,带电量+0.004C,重力加速度取10m/S2,将这个小球从地面向着与水平成45度角向右上方以10m/S的初速度抛出,求小球落地点距抛出点的距离.
分析:小球在重力场和电场的复合场中运动,运用运动的分解法研究.小球在水平方向做匀加速运动,竖直方向做竖直上抛运动,先根据竖直上抛运动的规律求出运动时间,进而求得水平位移.
解答:解:小球在竖直方向上做初速度大小为 vy=v0sin45°的竖直上抛运动,则根据运动的对称性可知:
小球运动的时间为 t=
=
;
在水平方向上,小球受到方向向右的电场力做匀加速直线运动,则小球落地点距抛出点的距离为:
x=v0cos45°t+
at2=v0cos45°t+
?
t2;
联立两式得:x=v0cos45°?
+
(
)2=[
+10×
×(
)2]m=20m;
答:小球落地点距抛出点的距离是20m.
小球运动的时间为 t=
| 2vy |
| g |
| 2v0sin45° |
| g |
在水平方向上,小球受到方向向右的电场力做匀加速直线运动,则小球落地点距抛出点的距离为:
x=v0cos45°t+
| 1 |
| 2 |
| 1 |
| 2 |
| qE |
| m |
联立两式得:x=v0cos45°?
| 2v0sin45° |
| g |
| qE |
| 2m |
| 2v0sin45° |
| g |
| 102sin90° |
| 10 |
| 0.004×50 |
| 2×20×10-3 |
| 2×10×sin45° |
| 10 |
答:小球落地点距抛出点的距离是20m.
点评:本题曲线运动动力学问题,采用与类平抛运动类似的研究方法:运动的分解法,同时要明确力作用的独立性,把握两个分运动的时间相等这一特点.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 如图所示,水平绝缘光滑轨道AB的B端与处于竖直平面内的四分之一圆弧形粗糙绝缘轨道BC平滑连接,圆弧的半径R=0.40m.在轨道所在空间存在水平向右的匀强电场,电场强度E=1.0×104 N/C.现有一质量m=0.10kg的带电体(可视为质点)放在水平轨道上与B端距离s=1.0m的位置,由于受到电场力的作用带电体由静止开始运动,当运动到圆弧形轨道的C端时,速度恰好为零.已知带电体所带电荷q=8.0×10-5C,取g=10m/s2,求:
如图所示,水平绝缘光滑轨道AB的B端与处于竖直平面内的四分之一圆弧形粗糙绝缘轨道BC平滑连接,圆弧的半径R=0.40m.在轨道所在空间存在水平向右的匀强电场,电场强度E=1.0×104 N/C.现有一质量m=0.10kg的带电体(可视为质点)放在水平轨道上与B端距离s=1.0m的位置,由于受到电场力的作用带电体由静止开始运动,当运动到圆弧形轨道的C端时,速度恰好为零.已知带电体所带电荷q=8.0×10-5C,取g=10m/s2,求: 如图所示,ACB为光滑圆弧轨道其半径为R,O为其圆心,OD为水平台面.AF为光滑水平面且与圆弧ACB光滑连接.已知:在DFAO区域存在水平向左的匀强电场,场强大小为E1,AOB右侧空间存在水平向右的匀强电场,场强大小为E2,且E1=E2.在AE水平面上有一个质量为m,电荷量为q的带负电小球(可看作质点).若其重力mg=qE1 问
如图所示,ACB为光滑圆弧轨道其半径为R,O为其圆心,OD为水平台面.AF为光滑水平面且与圆弧ACB光滑连接.已知:在DFAO区域存在水平向左的匀强电场,场强大小为E1,AOB右侧空间存在水平向右的匀强电场,场强大小为E2,且E1=E2.在AE水平面上有一个质量为m,电荷量为q的带负电小球(可看作质点).若其重力mg=qE1 问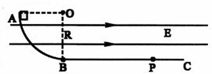 (2009?天津模拟)如图所示,竖直面内有一绝缘轨道,AB部分是光滑的四分之一圆弧,圆弧半径R=0.5m,B处切线水平,BC部分为水平粗糙直轨道.有一个带负电的小滑块(可视为质点)从A点由静止开始下滑,运动到直轨道上的P处刚好停住.小滑块的质量m=1kg,带电量为q=-2.5×10-3C保持不变,滑块小轨道BC部分间的动摩擦因数为μ=0.2,整个空间存在水平向右的匀强电场,电场强度大小为E=4.0×102N/C.(g=10m/s2)
(2009?天津模拟)如图所示,竖直面内有一绝缘轨道,AB部分是光滑的四分之一圆弧,圆弧半径R=0.5m,B处切线水平,BC部分为水平粗糙直轨道.有一个带负电的小滑块(可视为质点)从A点由静止开始下滑,运动到直轨道上的P处刚好停住.小滑块的质量m=1kg,带电量为q=-2.5×10-3C保持不变,滑块小轨道BC部分间的动摩擦因数为μ=0.2,整个空间存在水平向右的匀强电场,电场强度大小为E=4.0×102N/C.(g=10m/s2)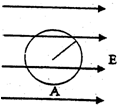 半径为r的绝缘光滑圆环固定在竖直平面内,环上套有质量为m、带正电的珠子,空间存在水平向右的匀强电场,如图所示,珠子所受静电力是其重力的
半径为r的绝缘光滑圆环固定在竖直平面内,环上套有质量为m、带正电的珠子,空间存在水平向右的匀强电场,如图所示,珠子所受静电力是其重力的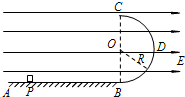 如图所示,水平绝缘轨道AB与处于竖直平面内的半圆形绝缘光滑轨道BC平滑连接,半圆形轨道的半径R=0.40m.轨道所在空间存在水平向右的匀强电场,电场强度E=1.0×104N/C.现有一电荷量q=+1.0×10-4C,质量m=0.10kg的带电体(可视为质点),在水平轨道上的P点由静止释放,带电体运动到圆形轨道最低点B时的速度vB=5.0m/s.已知带电体与水平轨道间的动摩擦因数μ=0.50,重力加速度g=10m/s2.求:
如图所示,水平绝缘轨道AB与处于竖直平面内的半圆形绝缘光滑轨道BC平滑连接,半圆形轨道的半径R=0.40m.轨道所在空间存在水平向右的匀强电场,电场强度E=1.0×104N/C.现有一电荷量q=+1.0×10-4C,质量m=0.10kg的带电体(可视为质点),在水平轨道上的P点由静止释放,带电体运动到圆形轨道最低点B时的速度vB=5.0m/s.已知带电体与水平轨道间的动摩擦因数μ=0.50,重力加速度g=10m/s2.求: