题目内容
【题目】如图所示，竖直圆环中有多条起始于A点的光滑轨道，其中AB通过环心O并保持竖直，一质点分别自A点沿各条轨道下滑，初速度均为零，那么，质点沿各轨道下滑的时间相比较错误的是（ ）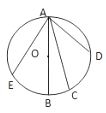
A.质点沿着与AB夹角越大的轨道下滑，时间越短
B.质点沿着轨道AB下滑，时间最短
C.轨道与AB夹角越小（AB除外），质点沿其下滑的时间越短
D.无论沿图中哪条轨道下滑，所用的时间均相同
【答案】A,B,C
【解析】解：设半径为R，斜面与竖直方向夹角为θ，则物体运动的位移为x=2Rcosθ，物体运动的加速度a= 
=gcosθ，
根据位移时间关系可得：x= 
at2，
解得：t= 
，与θ角无关．即与弦长无关，无论沿图中哪条轨道下滑，所用的时间均相同；
所以D正确，ABC错误．
本题选错误的，故选：ABC．
【考点精析】认真审题，首先需要了解匀变速直线运动的速度、位移、时间的关系(速度公式：V=V0+at；位移公式：s=v0t+1/2at2；速度位移公式：vt2-v02=2as；以上各式均为矢量式，应用时应规定正方向，然后把矢量化为代数量求解，通常选初速度方向为正方向，凡是跟正方向一致的取“+”值，跟正方向相反的取“-”值)．
练习册系列答案
相关题目
存在关系式
