��Ŀ����
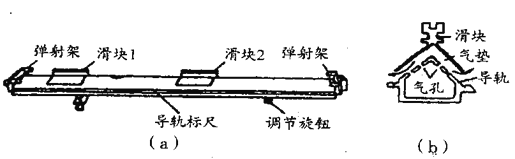
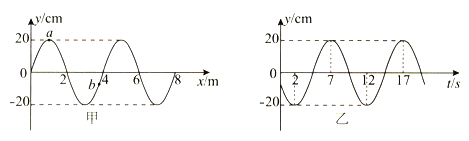
����Ŀ����ͼ��ʾ���̶�����ֱƽ���ڰ뾶ΪR���ķ�֮һ�⻬Բ�������ˮƽ�⻬���ƽ�����ӣ�A��B��C��������������Ϊm��B��C����ͬ�ֵ��������㹻Զ����ֹ��ˮƽ����ϵ�ͼʾλ�ã�������Ļ���A��Բ���ϵ�P���ɾ�ֹ���£�P�㴦�뾶��ˮƽ���30��ǣ�����B����������ճ�ϣ�Ȼ����B��C����������ֱ����C�����˶�����
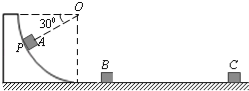
��A��Bճ�Ϻ���ٶȴ�С��
��A��Bճ�Ϻ�����C������ʱϵͳ�����ܵı仯��
���𰸡���A��Bճ�Ϻ���ٶȴ�С��![]() ��
��
��A��Bճ�Ϻ�����C������ʱϵͳ�����ܵ�������Ϊ ![]() mgR
mgR
��������
���������1��������P���µ���B��ײǰ�����ݶ��ܶ��������ײǰ���ٶȣ�����A��B��ײ���̶����غ����A��Bճ�Ϻ���ٶȴ�С��
2����B��C�ﵽ��ͬ�ٶ�ʱ��B��C����������ϵͳ�����غ㶨�����������ʱ���ٶȣ����������غ㶨�����ϵͳ�����ܵı仯��
�⣺�ٻ�����P���µ���B��ײǰ�����ݶ��ܶ����ã�
mgR��1��sin30�㣩=![]() mv2
mv2
�涨����Ϊ��������A��B��ײ���̶����غ�ã�
mv=2mv1
��ã�v1=![]()
�ڵ�B��C�ﵽ��ͬ�ٶ�ʱ��B��C���������涨����Ϊ��������ϵͳ�����غ㶨�ɵã�
2mv1=3mv2
���������غ㶨�ɣ�ϵͳ��ʧ�Ļ�е��ת��Ϊϵͳ�ĵ����ܣ����У�
��Ep=![]() ��2m
��2m![]() ��
��![]() ��3m
��3m![]()
�����ܵ�������Ϊ����Ep=![]() mgR
mgR
�𣺢�A��Bճ�Ϻ���ٶȴ�С��![]() ��
��
��A��Bճ�Ϻ�����C������ʱϵͳ�����ܵ�������Ϊ ![]() mgR��
mgR��