题目内容
17.用如图所示的装置测量某种矿物质的密度,操作步骤和实验数据如下:a.打开阀门K,使管A、容器C、容器B和大气相通.上下移动使水银面与刻度n对齐;
b.关闭K,向上举D,使水银面达到刻度ri处.这时测得B、D两管内水银面高度差h1=19.0cm;
c.打开K,把m=400g的矿物质投入C中,上下移动D,使水银面重新与n对齐,然后关闭K;
d.向上举,使水银面重新到达刻度m处,这时测得B、D两管内水银面高度差h2=20.6cm.
已知容器C和管A的总容积为VC=1000cm3,温度保持不变,求该矿物质的密度.
分析 整个过程都是等温变化,确定三个状态和各状态下的状态参量,根据理想气体等温变化列式即可求得结果.
解答 解:设水银的密度为ρ,大气压强为p0,容器B体积为VB,矿物体积V.VC=1000cm3=1×10-3m3
以C、A、B中封闭的气体为研究对象,以封闭时水银面处于n处为初状态,以水银面调至m处为末状态.由玻意耳定律得:
p0(VB+VC)=(p0+ρgh1)VC,
以C中装入矿物质后C、A、B中气体为研究对象,以封闭时水银面处于n处为初状态,以水银面调至m处为末状态.由玻意耳定律得:
p0(VB+VC-V)=(p0+ρgh2)(VC-V),
质量:m=ρV,
解得:ρ=$\frac{m}{V}$=$\frac{0.4kg}{7.77×1{0}^{-5}{m}^{3}}$≈5.15×103kg/m3;
答:该矿物质的密度为5.15×103kg/m3.
点评 该题考查了理想气体等温变化,解题的关键是确定气体状态和分析状态参量,体积的分析是解答该题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
12.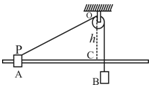 如图所示,水平光滑长杆上套有小物块A,细线跨过O点的轻质光滑小定滑轮一端连接A,另一端悬挂小物块B,物块A、B质量相等.C为0点正下方杆上一点,滑轮到杆的距离OC=h.开始时,A位于P点,PO与水平方向的夹角为30°.现将A、B静止释放.下列说法正确的是( )
如图所示,水平光滑长杆上套有小物块A,细线跨过O点的轻质光滑小定滑轮一端连接A,另一端悬挂小物块B,物块A、B质量相等.C为0点正下方杆上一点,滑轮到杆的距离OC=h.开始时,A位于P点,PO与水平方向的夹角为30°.现将A、B静止释放.下列说法正确的是( )
 如图所示,水平光滑长杆上套有小物块A,细线跨过O点的轻质光滑小定滑轮一端连接A,另一端悬挂小物块B,物块A、B质量相等.C为0点正下方杆上一点,滑轮到杆的距离OC=h.开始时,A位于P点,PO与水平方向的夹角为30°.现将A、B静止释放.下列说法正确的是( )
如图所示,水平光滑长杆上套有小物块A,细线跨过O点的轻质光滑小定滑轮一端连接A,另一端悬挂小物块B,物块A、B质量相等.C为0点正下方杆上一点,滑轮到杆的距离OC=h.开始时,A位于P点,PO与水平方向的夹角为30°.现将A、B静止释放.下列说法正确的是( )| A. | 物块A由P点出发第一次到达C点过程中,速度不断增大 | |
| B. | 在物块A由P点出发第一次到达C点过程中,物块B克服细线拉力做的功小于B重力势能的减少量 | |
| C. | 物块A在杆上长为2$\sqrt{3}$h的范围内做往复运动 | |
| D. | 物块A经过C点时的速度大小为$\sqrt{2gh}$ |
2. 如图所示是甲、乙两物体从同一地点同时沿同一方向运动的速度时间图象,其中t2=2t1,则( )
如图所示是甲、乙两物体从同一地点同时沿同一方向运动的速度时间图象,其中t2=2t1,则( )
 如图所示是甲、乙两物体从同一地点同时沿同一方向运动的速度时间图象,其中t2=2t1,则( )
如图所示是甲、乙两物体从同一地点同时沿同一方向运动的速度时间图象,其中t2=2t1,则( )| A. | 在t1时刻,乙物体在前,甲物体在后 | |
| B. | 在t1时刻,甲、乙两物体相遇 | |
| C. | 在t1时刻,甲、乙两物体速度相等,且两物体相距最远 | |
| D. | 在t2时刻,甲、乙两物体相遇 |
9. 如图所示,足够长的光滑三角形绝缘槽,与水平面的夹角分别为α和β(α<β),加垂直于纸面向里的磁场.分别将质量相等、带等量正、负电荷的小球 a、b依次从两斜面的顶端由静止释放,关于两球在槽上运动的说法不正确的是( )
如图所示,足够长的光滑三角形绝缘槽,与水平面的夹角分别为α和β(α<β),加垂直于纸面向里的磁场.分别将质量相等、带等量正、负电荷的小球 a、b依次从两斜面的顶端由静止释放,关于两球在槽上运动的说法不正确的是( )
 如图所示,足够长的光滑三角形绝缘槽,与水平面的夹角分别为α和β(α<β),加垂直于纸面向里的磁场.分别将质量相等、带等量正、负电荷的小球 a、b依次从两斜面的顶端由静止释放,关于两球在槽上运动的说法不正确的是( )
如图所示,足够长的光滑三角形绝缘槽,与水平面的夹角分别为α和β(α<β),加垂直于纸面向里的磁场.分别将质量相等、带等量正、负电荷的小球 a、b依次从两斜面的顶端由静止释放,关于两球在槽上运动的说法不正确的是( )| A. | 在槽上,a、b两球都做匀加速直线运动,且aa>ab | |
| B. | a、b两球沿槽运动的最大速度为va和vb,则va>vb | |
| C. | a、b两球沿直槽运动的最大位移为Sa和Sb,则Sa<Sb | |
| D. | a、b两球沿槽运动的时间为ta和tb,则ta<tb |
6. 如图所示,物体a、b从水平地面上的不同位置斜向上抛出,最终落在水平地面上的同一点,两条路径的最高点是等高的.忽略空气阻力,下列说法正确的是( )
如图所示,物体a、b从水平地面上的不同位置斜向上抛出,最终落在水平地面上的同一点,两条路径的最高点是等高的.忽略空气阻力,下列说法正确的是( )
 如图所示,物体a、b从水平地面上的不同位置斜向上抛出,最终落在水平地面上的同一点,两条路径的最高点是等高的.忽略空气阻力,下列说法正确的是( )
如图所示,物体a、b从水平地面上的不同位置斜向上抛出,最终落在水平地面上的同一点,两条路径的最高点是等高的.忽略空气阻力,下列说法正确的是( )| A. | a、b在最高点的速度相同 | B. | a、b在单位时间内速度变化量相同 | ||
| C. | a运动的时间比b运动的时间长 | D. | a落地的速率比b落地的速率大 |
 如图所示,质量为m的长木板静置于光滑水平面,质量为3m的物块以速度v水平冲上木板左端,物块与木板之间的动摩擦因数为μ.在水平面的右侧有一固定的竖直墙壁,木板每次与墙壁碰撞均为弹性碰撞.已知木板第一次与墙壁碰撞前物块已相对木板静止.设木板足够长,物块始终在木板上,重力加速度为g,求:
如图所示,质量为m的长木板静置于光滑水平面,质量为3m的物块以速度v水平冲上木板左端,物块与木板之间的动摩擦因数为μ.在水平面的右侧有一固定的竖直墙壁,木板每次与墙壁碰撞均为弹性碰撞.已知木板第一次与墙壁碰撞前物块已相对木板静止.设木板足够长,物块始终在木板上,重力加速度为g,求: