题目内容
12.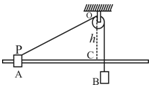 如图所示,水平光滑长杆上套有小物块A,细线跨过O点的轻质光滑小定滑轮一端连接A,另一端悬挂小物块B,物块A、B质量相等.C为0点正下方杆上一点,滑轮到杆的距离OC=h.开始时,A位于P点,PO与水平方向的夹角为30°.现将A、B静止释放.下列说法正确的是( )
如图所示,水平光滑长杆上套有小物块A,细线跨过O点的轻质光滑小定滑轮一端连接A,另一端悬挂小物块B,物块A、B质量相等.C为0点正下方杆上一点,滑轮到杆的距离OC=h.开始时,A位于P点,PO与水平方向的夹角为30°.现将A、B静止释放.下列说法正确的是( )| A. | 物块A由P点出发第一次到达C点过程中,速度不断增大 | |
| B. | 在物块A由P点出发第一次到达C点过程中,物块B克服细线拉力做的功小于B重力势能的减少量 | |
| C. | 物块A在杆上长为2$\sqrt{3}$h的范围内做往复运动 | |
| D. | 物块A经过C点时的速度大小为$\sqrt{2gh}$ |
分析 在绳子作用下物块A由P点到C点的过程,绳子的拉力做正功,速度增大.到C点时B的速度为零.根据能量守恒定律,分析物块B克服细线拉力做的功与B重力势能的减少量的关系.结合对称性分析物块A的运动范围.由系统的机械能守恒求物块经过C点时的速度.
解答 解:A、物块A由P点出发第一次到达C点过程中,绳子拉力对A做正功,动能不断增大,速度不断增大,故A正确.
B、到C点时B的速度为零.则根据功能关系可知,在物块A由P点出发第一次到达C点过程中,物块B克服细线拉力做的功等于B重力势能的减少量,故B错误.
C、由几何知识可得 $\overline{AC}$=$\sqrt{3}$h,由于AB组成的系统机械能守恒,由对称性可得物块A在杆上长为2$\sqrt{3}$h的范围内做往复运动.故C正确.
D、设物块A经过C点时的速度大小为v,此时B的速度为0.
根据系统的机械能守恒得:mg($\frac{h}{sin30°}$-h)=$\frac{1}{2}m{v}^{2}$,得 v=$\sqrt{2gh}$,故D正确.
故选:ACD.
点评 本题的关键要正确分析两物块的运动情况,知道当A的速度最大时,B的速度为零,明确系统遵守机械能守恒,但对单个物块而言,机械能是不守恒的.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
3.(多选)唱卡拉OK用的动圈式话筒,它的工作原理是在弹性膜片后面黏接一个轻小的闭合金属线圈,线圈处于永磁体的磁场中,当声波使膜片前后振动是,就将声音信号转变为电信号.下列说法正确的是( )
| A. | 该话筒是根据电流的磁效应工作的 | |
| B. | 该话筒是根据电磁感应原理工作的 | |
| C. | 膜片振动时,穿过线圈的磁通量不变 | |
| D. | 膜片振动时,金属线圈中产生感应电流 |
20.如图所示,在下列各个表示物体运动规律的图象中,表示同一运动规律的是( )


| A. | 甲图和丙图 | B. | 甲图和丁图 | C. | 乙图和丙图 | D. | 乙图和丁图 |
7. 在t=0时,甲、乙两质点从相距70m的两地开始相向运动,它们的v-t图象如图所示.下列说法正确的是( )
在t=0时,甲、乙两质点从相距70m的两地开始相向运动,它们的v-t图象如图所示.下列说法正确的是( )
 在t=0时,甲、乙两质点从相距70m的两地开始相向运动,它们的v-t图象如图所示.下列说法正确的是( )
在t=0时,甲、乙两质点从相距70m的两地开始相向运动,它们的v-t图象如图所示.下列说法正确的是( )| A. | 前4s内,乙质点的加速度始终大于甲质点 | |
| B. | 第1s末,乙质点改变运动方向 | |
| C. | 第3s末,甲、乙两质点相遇 | |
| D. | 第4s末,甲、乙两质点相距30m |
4.在“探究弹力和弹簧伸长的关系”实验中,以下说法正确的是 ( )
| A. | 弹簧被拉伸时,不能超出它的弹性限度 | |
| B. | 弹簧的弹力大小与弹簧的长度成正比 | |
| C. | 用直尺测得弹簧的长度即为弹簧的伸长量 | |
| D. | 用几个不同的弹簧,分别测出几组拉力与伸长量,得出拉力与伸长量之比均相等. |
1.1834年,楞次在分析了许多实验事实后,用一句话巧妙地概括出感应电流方向遵循的规律.在做用条形磁铁穿过闭合导体线圈的探究实验中,以下描述符合客观事实的是( )
| A. | 线圈内感应电流产生的磁场方向总是与条形磁铁产生的磁场方向相反 | |
| B. | 线圈内感应电流产生的磁场方向总是与条形磁铁产生的磁场方向相同 | |
| C. | 线圈内感应电流产生的磁场方向总是与条形磁铁产生的磁场方向先相反后形同 | |
| D. | 线圈内感应电流产生的磁场方向总是与条形磁铁产生的磁场方向先相同后相反 |
2. 在匀强磁场里有一个原来静止的放射性碳14,它所放射的粒子与反冲核的轨迹是两个相切的圆,圆的半径比为5:1,那么碳的衰变方程是( )
在匀强磁场里有一个原来静止的放射性碳14,它所放射的粒子与反冲核的轨迹是两个相切的圆,圆的半径比为5:1,那么碳的衰变方程是( )
 在匀强磁场里有一个原来静止的放射性碳14,它所放射的粒子与反冲核的轨迹是两个相切的圆,圆的半径比为5:1,那么碳的衰变方程是( )
在匀强磁场里有一个原来静止的放射性碳14,它所放射的粒子与反冲核的轨迹是两个相切的圆,圆的半径比为5:1,那么碳的衰变方程是( )| A. | ${\;}_{6}^{14}$C→${\;}_{2}^{4}$He+${\;}_{4}^{10}$Be | B. | ${\;}_{6}^{14}$C→${\;}_{1}^{0}$e+${\;}_{5}^{14}$B | ||
| C. | ${\;}_{6}^{14}$C→${\;}_{-1}^{0}$e+${\;}_{7}^{14}$N | D. | ${\;}_{6}^{14}$C→${\;}_{1}^{2}$H+${\;}_{5}^{12}$B |
 如图所示,物重100N,用OC绳悬挂在O点,在拉力F的作用下,静止于结点A,此时绳与竖直方向的夹角θ=37°,求:
如图所示,物重100N,用OC绳悬挂在O点,在拉力F的作用下,静止于结点A,此时绳与竖直方向的夹角θ=37°,求: