题目内容
9.质量为m的物体,在距水平地面h高处以$\frac{g}{4}$的加速度匀加速竖直下落到地面,若重力加速度为g,则在此过程中( )| A. | 物体的重力势能减少mgh | B. | 物体的动能增加mgh | ||
| C. | 物体的机械能减少$\frac{1}{4}$mgh | D. | 物体的机械能减少$\frac{3}{4}$mgh |
分析 对物体受力分析,受重力G和向上的外力F,根据牛顿第二定律列式求出各个力,然后根据功能关系得到各种能量的变化情况.
解答 解:物体从距地面h高处由静止开始以加速度a=$\frac{g}{4}$竖直下落,
根据牛顿第二定律得:ma=mg-F阻,得:
物体受到的阻力:F阻=$\frac{3}{4}$mg
A、物体下降,重力做正功mgh,则物体重力势能减少了mgh,故A正确;
B、由动能定理得:F合h=Ek-0,
又F合=ma=$\frac{1}{4}$mg
解得Ek=$\frac{1}{4}$mgh,故B错误;
C、D、物体重力势能减少了mgh,动能增加了$\frac{1}{4}$mg,故机械能减少了$\frac{3}{4}$mgh,故C错误,D正确;
故选:AD
点评 本题关键对物体受力分析,然后根据牛顿第二定律列式求出外F,最后根据动能定理和重力做功和重力势能变化的关系列方程求解.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
8.高空作业须系安全带,如果质量为m的高空作业人员不慎跌落,从开始跌落到安全带对人刚刚产生作用前人下落的距离为h(可视为自由落体运动).此后经历时间t安全带达到最大伸长,若在此过程中该作用力始终竖直向上,则该段时间安全带对人的平均作用力大小为( )
| A. | $\frac{m\sqrt{2gh}}{t}$+mg | B. | $\frac{m\sqrt{2gh}}{t}$-mg | C. | $\frac{m\sqrt{gh}}{t}$+mg | D. | $\frac{m\sqrt{gh}}{t}$-mg |
4.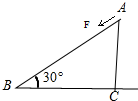 如图所示,水平面上固定有高为AC=H、倾角为30°的直角三角形光滑斜面,有一长为2H、质量为m的均匀绳,其一端拴有质量为m(可看作质点)的小球,另一端在外力F作用下通过斜面顶端的光滑小定滑轮从A点沿斜面缓慢运动到B点,不计绳绷紧是的能量损失,则该过程中( )
如图所示,水平面上固定有高为AC=H、倾角为30°的直角三角形光滑斜面,有一长为2H、质量为m的均匀绳,其一端拴有质量为m(可看作质点)的小球,另一端在外力F作用下通过斜面顶端的光滑小定滑轮从A点沿斜面缓慢运动到B点,不计绳绷紧是的能量损失,则该过程中( )
 如图所示,水平面上固定有高为AC=H、倾角为30°的直角三角形光滑斜面,有一长为2H、质量为m的均匀绳,其一端拴有质量为m(可看作质点)的小球,另一端在外力F作用下通过斜面顶端的光滑小定滑轮从A点沿斜面缓慢运动到B点,不计绳绷紧是的能量损失,则该过程中( )
如图所示,水平面上固定有高为AC=H、倾角为30°的直角三角形光滑斜面,有一长为2H、质量为m的均匀绳,其一端拴有质量为m(可看作质点)的小球,另一端在外力F作用下通过斜面顶端的光滑小定滑轮从A点沿斜面缓慢运动到B点,不计绳绷紧是的能量损失,则该过程中( )| A. | 绳子的重力做功为0 | B. | 绳的重力势能增加了$\frac{1}{4}$mgH | ||
| C. | 绳的机械能增加了$\frac{1}{4}$mgH | D. | 小球对绳的拉力做功mgH |
18.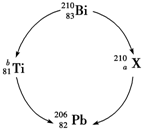 ${\;}_{92}^{238}$U放射性衰变有多种可能途径,其中一种途径是先变成${\;}_{83}^{210}$Bi,而${\;}_{83}^{210}$Bi可以经一次衰变变成${\;}_{a}^{210}$X(X代表某种元素),也可以经一次衰变变成${\;}_{81}^{b}$Ti,${\;}_{a}^{210}$X和${\;}_{81}^{b}$Ti最后都变成${\;}_{82}^{206}$Pb,衰变路径如图所示,则( )
${\;}_{92}^{238}$U放射性衰变有多种可能途径,其中一种途径是先变成${\;}_{83}^{210}$Bi,而${\;}_{83}^{210}$Bi可以经一次衰变变成${\;}_{a}^{210}$X(X代表某种元素),也可以经一次衰变变成${\;}_{81}^{b}$Ti,${\;}_{a}^{210}$X和${\;}_{81}^{b}$Ti最后都变成${\;}_{82}^{206}$Pb,衰变路径如图所示,则( )
 ${\;}_{92}^{238}$U放射性衰变有多种可能途径,其中一种途径是先变成${\;}_{83}^{210}$Bi,而${\;}_{83}^{210}$Bi可以经一次衰变变成${\;}_{a}^{210}$X(X代表某种元素),也可以经一次衰变变成${\;}_{81}^{b}$Ti,${\;}_{a}^{210}$X和${\;}_{81}^{b}$Ti最后都变成${\;}_{82}^{206}$Pb,衰变路径如图所示,则( )
${\;}_{92}^{238}$U放射性衰变有多种可能途径,其中一种途径是先变成${\;}_{83}^{210}$Bi,而${\;}_{83}^{210}$Bi可以经一次衰变变成${\;}_{a}^{210}$X(X代表某种元素),也可以经一次衰变变成${\;}_{81}^{b}$Ti,${\;}_{a}^{210}$X和${\;}_{81}^{b}$Ti最后都变成${\;}_{82}^{206}$Pb,衰变路径如图所示,则( )| A. | a=82,b=211 | |
| B. | ${\;}_{83}^{210}$Bi→${\;}_{a}^{210}$X是β衰变,${\;}_{83}^{210}$Bi→${\;}_{81}^{b}$Ti是α衰变 | |
| C. | ${\;}_{83}^{210}$Bi→${\;}_{a}^{210}$X是α衰变,${\;}_{83}^{210}$Bi→${\;}_{81}^{b}$Ti是β衰变 | |
| D. | ${\;}_{81}^{b}$Ti经过一次β衰变变成${\;}_{82}^{206}$Pb |
19.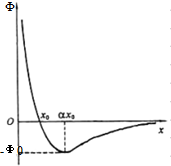 两个点电荷位于x轴上,在它们形成的电场中,若取无限远处的电势为零,则在正x轴上各点的电势如图中曲线所示.电势为零的点的坐标x0,电势为极小值-Φ0的点的坐标为ax0(a>2).(已知点电荷的电场中各点的电势Φ=k$\frac{Q}{r}$,式中Q为点电荷的电量,r为距点电荷的距离)根据图线提供的信息,以下说法正确的是( )
两个点电荷位于x轴上,在它们形成的电场中,若取无限远处的电势为零,则在正x轴上各点的电势如图中曲线所示.电势为零的点的坐标x0,电势为极小值-Φ0的点的坐标为ax0(a>2).(已知点电荷的电场中各点的电势Φ=k$\frac{Q}{r}$,式中Q为点电荷的电量,r为距点电荷的距离)根据图线提供的信息,以下说法正确的是( )
 两个点电荷位于x轴上,在它们形成的电场中,若取无限远处的电势为零,则在正x轴上各点的电势如图中曲线所示.电势为零的点的坐标x0,电势为极小值-Φ0的点的坐标为ax0(a>2).(已知点电荷的电场中各点的电势Φ=k$\frac{Q}{r}$,式中Q为点电荷的电量,r为距点电荷的距离)根据图线提供的信息,以下说法正确的是( )
两个点电荷位于x轴上,在它们形成的电场中,若取无限远处的电势为零,则在正x轴上各点的电势如图中曲线所示.电势为零的点的坐标x0,电势为极小值-Φ0的点的坐标为ax0(a>2).(已知点电荷的电场中各点的电势Φ=k$\frac{Q}{r}$,式中Q为点电荷的电量,r为距点电荷的距离)根据图线提供的信息,以下说法正确的是( )| A. | 可以确定这两个点电荷必为异种电荷 | |
| B. | 可以求出这两个点电荷的电量大小 | |
| C. | 可以求出这两个点电荷在x轴上的位置坐标 | |
| D. | 可以确定x轴上各点的电场强度均沿+x方向 |
 如图所示,竖直放置的足够长的光滑平行金属导轨,间距为L=0.50m,导轨上端接有电阻R=0.80Ω,导轨电阻忽略不计.空间有一水平方向的有理想上边界的匀强磁场,磁感应强度B=0.40T、方向垂直于金属导轨平面向外,质量为m=0.02kg、电阻r=0.20Ω的金属杆MN,从静止开始沿着金属导轨下落.以v0=2.5m/s的速度进入匀强磁场中,在磁场中下落H=4m时开始匀速运动,下落过程中金属刚始终与两导轨垂直且接触良好,重力加速度g=10m/s2,不计空气阻力.
如图所示,竖直放置的足够长的光滑平行金属导轨,间距为L=0.50m,导轨上端接有电阻R=0.80Ω,导轨电阻忽略不计.空间有一水平方向的有理想上边界的匀强磁场,磁感应强度B=0.40T、方向垂直于金属导轨平面向外,质量为m=0.02kg、电阻r=0.20Ω的金属杆MN,从静止开始沿着金属导轨下落.以v0=2.5m/s的速度进入匀强磁场中,在磁场中下落H=4m时开始匀速运动,下落过程中金属刚始终与两导轨垂直且接触良好,重力加速度g=10m/s2,不计空气阻力.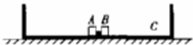 如图所示,在光滑的水平桌面上有一长为L=2m的木板C,它的两端各有一块挡板,C连同挡板的总质量为mC=5kg,在C的中央并排放着两个可视为质点的滑块A与B,其质量分别为mA=1kg、mB=4kg,开始时A、B、C均处于静止状态,并且A、B间夹有少许炸药,炸药爆炸使得A以vA=6m/s的速度水平向左运动,不计一切摩擦,两滑块中任一块与挡板碰撞后就与挡板合成一体,爆炸与碰撞时间不计,求:
如图所示,在光滑的水平桌面上有一长为L=2m的木板C,它的两端各有一块挡板,C连同挡板的总质量为mC=5kg,在C的中央并排放着两个可视为质点的滑块A与B,其质量分别为mA=1kg、mB=4kg,开始时A、B、C均处于静止状态,并且A、B间夹有少许炸药,炸药爆炸使得A以vA=6m/s的速度水平向左运动,不计一切摩擦,两滑块中任一块与挡板碰撞后就与挡板合成一体,爆炸与碰撞时间不计,求: 如图所示,上表面水平的平板车B右端固定一轻质弹簧,平板车左端与弹簧的自由端相距L,开始时静止在光滑水平面上,在平板车最左端静止放置一小物块A,一颗质量为m0的子弹以水平初速度v0迅速射穿A后,速度变为$\frac{{v}_{0}}{2}$,子弹射穿前后物块A的质量不变.此后,物块A向右运动压缩弹簧后被弹回并停在小车最左端(弹簧始终在弹性限度内),已知平板车B质量为10m0,物块A质量为2m0.A、B之间的动摩擦因数为μ,重力加速度为g.求:
如图所示,上表面水平的平板车B右端固定一轻质弹簧,平板车左端与弹簧的自由端相距L,开始时静止在光滑水平面上,在平板车最左端静止放置一小物块A,一颗质量为m0的子弹以水平初速度v0迅速射穿A后,速度变为$\frac{{v}_{0}}{2}$,子弹射穿前后物块A的质量不变.此后,物块A向右运动压缩弹簧后被弹回并停在小车最左端(弹簧始终在弹性限度内),已知平板车B质量为10m0,物块A质量为2m0.A、B之间的动摩擦因数为μ,重力加速度为g.求: