题目内容
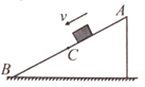
【题目】如图所示,位于竖直平面内的一长木板斜靠在竖直墙上的A点,其与水平面夹角为53°;另一个同样材料的长木板斜靠在竖直墙上的B点,其与水平面的夹角为45°;两长木板底端都在C点处。若将同一小滑块分别从A,B两点静止释放,小滑块经过相同时间运动到C点。(![]() )求:
)求:

(1)小滑块与长木板间的动摩擦因数的大小?
(2)若墙底部O点与C点间的距离L=0.7m,小滑块质量m=1kg,则小滑块从B下滑到C点时的动能是多少?
【答案】(1)![]() (2)
(2) ![]()
【解析】(1)设长木板与水平面间的夹角为α,根据牛顿第二定律分析可知,小滑块在长木板上的加速度大小为:a=gsin α-μgcos α,
设竖直墙壁到C点的距离为L,则长木板长度为:![]()
联立以上两式可得:(sin α-μcos α)cos α=![]()
根据题意:(sin 53°-μcos 53°)cos 53°=(sin 45°-μcos 45°)cos 45°
解得μ=1/7
(2)设小滑块滑到从B滑到C点时动能为EK,则
EK=mgLtan45°-μmgcos 45°![]()
![]()
解得EK=6J

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目