题目内容
【题目】如图为一压路机的示意图,其大轮半径是小轮半径的1.5倍,A、B分别为大轮和小轮边缘上的点,在压路机前进时( )
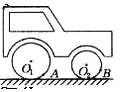
A.A、B两点的转速之比nA∶nB = 1∶1
B.A、B两点的线速度之比vA∶vB= 3∶2
C.A、B两点的角速度之比ωA∶ωB = 3∶2
D.A、B两点的向心加速度之比aA∶aB = 2∶3
【答案】D
【解析】
试题分析:压路机前进时,其轮子边缘上的点参与两个分运动,即绕轴心的转动和随着车的运动;与地面接触点速度为零,故两个分运动的速度大小相等、方向相反,故A、B两点圆周运动的线速度都等于汽车前进的速度,故A、B两点的线速度之比vA:vB=1:1,根据v=2πr n可知转速之比为2:3,故AB错误;A、B两点的线速度之比vA:vB=1:1,根据公式v=rω,线速度相等时,角速度与半径成反比,故A、B两点的角速度之比ωA:ωB=2:3,故C错误;根据a= vω可知A、B两点的向心加速度之比aA∶aB = 2∶3,选项D正确;故选D。

练习册系列答案
相关题目