��Ŀ����
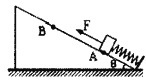
����Ŀ����ͼ��ʾ��һ�̶�ֱ��AB��ΪL=2m������ֱ����ļн�Ϊ��=53����һ����Ϊm=4kg�������Ϊq=+3��10-5 C��С������ֱ���ϣ���С���A�˾�ֹ�ͷţ�����˼�Ķ�Ħ������Ϊ��=![]() ��ֱ�����ڴ��ռ���ˮƽ���ҵ���ǿ�糡����ǿΪE =1��106N/C���������ٶ�g=10m/s2
��ֱ�����ڴ��ռ���ˮƽ���ҵ���ǿ�糡����ǿΪE =1��106N/C���������ٶ�g=10m/s2
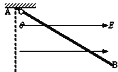
(1) ��С���»���������Ħ�����Ĵ�С
(2) ��С���»����˵�B��ʱ���ٶȴ�Сv1��
(3)������ֱ����ļнDz�ͬ��С�����˵�B��ʱ���ٶȴ�С��ͬ����������ֱ����ļн�Ϊijһֵʱ��С����B�˾��������ٶȣ���˼н��Լ���Ӧ��С����B�˵��ٶȴ�С��
���𰸡���1��12N��2��6m/s��3��5![]() m/s
m/s
����������1��С��������֪���糡��Ϊ��F=qE=3��10��5��106N=30N��
����Ϊ��N=mgsin�ȩ�Fcos��=��40��0.8��30��0.6��N=14N��
Ħ������СΪ��f=��N= ![]() ��14N=12N
��14N=12N
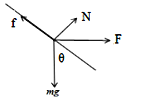
��2��С�����ߵ��˶�����͵�����У��ɶ��ܶ����ã�
��Fsin��+mgcos����f��L= ![]() mv12��0��
mv12��0��
�������ݿɽ�ã�v1=6m/s��
С���Ͷ�ʱ���ٶȴ�СΪ6m/s
��3��ΪʹС��B��ʱ���ٶ����������糡�����Ĺ������˷�Ħ�������Ĺ���СʱС����ٶ�������Ӧ��������糡���ĺ�������
��tan��= ![]() =
= ![]() ��
��
�������ֱ����нǣ���=37�㣬��ʱĦ����Ϊ0��
�ɶ��ܶ����ã���Fsin��+mgcos����L=![]() mv22��0��
mv22��0��
�������ݽ�ã�v2=5![]() m/s
m/s