题目内容
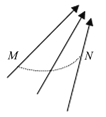
【题目】如图所示,AOB是截面为扇形的透明介质的横截面图,其圆心角∠AOB=90°,半径为r。在OA边的右半部分AD间有一束平行光线垂直OA边射入透明介质,已知透明介质对该光线的折射率n=![]() 。(对于某一光线有折射时不考虑反射)
。(对于某一光线有折射时不考虑反射)

①求圆弧面上有光线射出的弧长;
②某光线经圆弧面两次全反射后恰好垂直OB面射出,求出射点到O点的距离(可用三角函数表示)。
【答案】(1)![]() (2)rcos22.5°
(2)rcos22.5°
【解析】试题分析:根据![]() 求出临界角,画出光路图结合几何关系即可求出圆弧面上有光线射出的弧长和出射点到O点的距离。
求出临界角,画出光路图结合几何关系即可求出圆弧面上有光线射出的弧长和出射点到O点的距离。
①根据公式: ![]()
可得临界角:C=60°
即光线在圆弧面上的入射角等于60°时恰好发生全反射。如图所示,设光线从E点射入时,在F点恰好发生全反射,由几何关系可知∠FOA=30°,从F点反射的光线恰好从B点射出,所以圆弧面FI间均有光线射出,由几何关系可知

∠FOI=30°
圆弧面上有光线射出的弧长: ![]()
②设光线GH在圆弧面经过两次反射后恰好垂直OB射出,出射点到O点的距离为lCK,则有:∠AOH=∠JOB=![]() ∠HOJ
∠HOJ
而∠AOH+∠JOB+∠HOJ=90°
所以∠JOB=22.5°
lCK=rcos22.5°

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目