题目内容
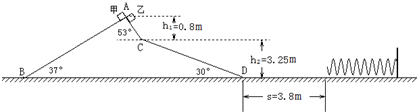
如图所示,静止在粗糙水平面上的斜面体有三个光滑斜面AB、AC和CD.已知斜面AB与水平方向成37°角,斜面AC与水平方向成53°角,斜面CD与水平方向成30°角,A点与C点的竖直高度为h1=0.8m,C点与D点的竖直高度为h2=3.25m.在B点左侧的水平面上有一个一端固定的轻质弹簧,自然长度时弹簧右端到B点的水平距离为s=3.9m.质量均为m=1kg的物体甲和乙同时从顶点A由静止释放,之后甲沿斜面AB下滑,乙沿AC下滑.在甲乙两物体下滑过程中,斜面体始终处于静止状态,且两物体运动中经过B点、C点、D点时,速度大小不改变,只改变方向.甲进入水平面后向左运动压缩弹簧的最大压缩量为x=0.1m,乙物体进入水平面后便向右运动最终停止.已知甲物体与水平面的动摩擦因数为μ=0.6,sin37°=0.6,cos37°=0.8,g取10m/s2.求:
(1)弹簧的最大弹性势能为多少?
(2)甲物体最终停止位置距B点多远?
(3)通过计算,说明甲乙两物体是否同时滑到水平面上?

(1)弹簧的最大弹性势能为多少?
(2)甲物体最终停止位置距B点多远?
(3)通过计算,说明甲乙两物体是否同时滑到水平面上?

分析:(1)当滑块甲运动到最左端时,弹簧的弹性势能最大,对滑块甲运用动能定理列式计算;
(2)先对整个运动过程运用动能定理列式求解出滑块相对于初潮地面的总路程,再根据几何关系得出甲物体最终停止位置距B点的距离;
(3)对甲受力分析后,根据牛顿第二定律求出加速度,然后根据位移时间公式求出时间t1;再对乙受力分析后求出加速度,再根据位移公式和速度时间公式求时间,最后比较是否同时.
(2)先对整个运动过程运用动能定理列式求解出滑块相对于初潮地面的总路程,再根据几何关系得出甲物体最终停止位置距B点的距离;
(3)对甲受力分析后,根据牛顿第二定律求出加速度,然后根据位移时间公式求出时间t1;再对乙受力分析后求出加速度,再根据位移公式和速度时间公式求时间,最后比较是否同时.
解答:解:(1)当滑块甲运动到最左端时,弹簧的弹性势能最大,对滑块甲从A到最左端过程运用动能定理,得到
mg(h1+h2)-μmg(S+x)-W弹=0-0
弹簧弹力做的功等于弹性势能增加量,故
Epm=W弹
解得
Epm=mg(h1+h2)-μmg(S+x)=1×10×(0.8+3.25)-0.6×1×10×(3.9+0.1)=16.5J
即弹簧的最大弹性势能为16.5J.
(2)对甲物体从开始到停止运动的整个过程运用动能定理,有
mg(h1+h2)-μmg?L=0-0
解得
L=
=6.75m
故甲物体最终停止位置距B点为:x1=2(h1+h2)-L=1.25m.
(3)甲物体受重力、支持力,根据牛顿第二定律,有
mgsin37°=ma1
根据位移时间公式,有
=
a1
解得
t1=1.5s
对于乙物体,在倾角为53°的斜面上时,加速度设为a2,在倾角为30°的斜面上时,加速度设为a3
根据牛顿第二定律,有
mgsin53°=ma2
mgsin30°=ma3
根据运动学公式,有
=
a2
v=a2t2
=vt3+
a3
解得
t2=0.5s
t3=1s
故t1=t2+t3
即甲乙两物体同时到达水平面上.
mg(h1+h2)-μmg(S+x)-W弹=0-0
弹簧弹力做的功等于弹性势能增加量,故
Epm=W弹
解得
Epm=mg(h1+h2)-μmg(S+x)=1×10×(0.8+3.25)-0.6×1×10×(3.9+0.1)=16.5J
即弹簧的最大弹性势能为16.5J.
(2)对甲物体从开始到停止运动的整个过程运用动能定理,有
mg(h1+h2)-μmg?L=0-0
解得
L=
| h1+h2 |
| μ |
故甲物体最终停止位置距B点为:x1=2(h1+h2)-L=1.25m.
(3)甲物体受重力、支持力,根据牛顿第二定律,有
mgsin37°=ma1
根据位移时间公式,有
| h1+h2 |
| sin37° |
| 1 |
| 2 |
| t | 2 1 |
解得
t1=1.5s
对于乙物体,在倾角为53°的斜面上时,加速度设为a2,在倾角为30°的斜面上时,加速度设为a3
根据牛顿第二定律,有
mgsin53°=ma2
mgsin30°=ma3
根据运动学公式,有
| h1 |
| sin53° |
| 1 |
| 2 |
| t | 2 2 |
v=a2t2
| h2 |
| sin30° |
| 1 |
| 2 |
| t | 2 3 |
解得
t2=0.5s
t3=1s
故t1=t2+t3
即甲乙两物体同时到达水平面上.
点评:本题关键灵活地选择过程运用动能定理列式求解;对斜面上的运动可以运用牛顿第二定律和运动学公式联立求解.

练习册系列答案
相关题目
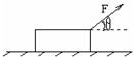 如图所示物体静止在粗糙水平面上,现对物体施加一个与水平方向成θ角的斜向上的拉力F,保持θ角不变,使F从零开始逐渐增大(物体始终未离开水平面),在此过程中物体受到的摩擦力将( )
如图所示物体静止在粗糙水平面上,现对物体施加一个与水平方向成θ角的斜向上的拉力F,保持θ角不变,使F从零开始逐渐增大(物体始终未离开水平面),在此过程中物体受到的摩擦力将( )| A、逐渐增大 | B、逐渐减小 | C、先逐渐增大后逐渐减小 | D、先逐渐减小后逐渐增大 |

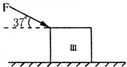 如图所示,静止在粗糙水平地面上的物体,质量为2kg,在斜向下与水平方向夹角为37°的推力F的推动下,物体开始运动,经过3.75s,物体的速度达15m/s;此时撤去外力F,又经过6s,物体停下.如果物体与地面间的动摩擦因素不变,求推力F的大小.(已知sin37°=0.6,cos37°=0.8,取g=10m/s2)
如图所示,静止在粗糙水平地面上的物体,质量为2kg,在斜向下与水平方向夹角为37°的推力F的推动下,物体开始运动,经过3.75s,物体的速度达15m/s;此时撤去外力F,又经过6s,物体停下.如果物体与地面间的动摩擦因素不变,求推力F的大小.(已知sin37°=0.6,cos37°=0.8,取g=10m/s2)