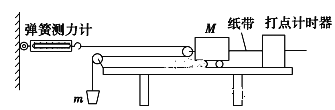
题目内容
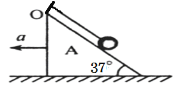
【题目】如图所示,光滑水平桌面上放置一个倾角为37°的光滑楔形滑块A,质量为M=0.8kg。一细线的一端固定于楔形滑块A的顶端O处,细线另一端拴一质量为m=0.2kg的小球。若滑块与小球在外力F作用下,一起以加速度a向左做匀加速运动。取g=10 m/s2;sin370=0.6;sin530=0.8,则下列说法正确的是( )
A.当a=5 m/s2时,滑块对球的支持力为0 NB.当a=15 m/s2时,滑块对球的支持力为0 N
C.当a=5 m/s2时,外力F的大小为4ND.当a=15 m/s2时,地面对A的支持力为10N
【答案】BD
【解析】
设加速度为a0时小球对滑块的压力等于零,对小球受力分析,受重力和拉力,
根据牛顿第二定律,有:
水平方向:![]() ,
,
竖直方向:![]() ,
,
解得![]()
A.当![]() 时,小球未离开滑块,斜面对小球的支持力不为零,选项A错误;
时,小球未离开滑块,斜面对小球的支持力不为零,选项A错误;
B.当![]() 时,小球已经离开滑块,只受重力和绳的拉力,滑块对球的支持力为零,选项B正确;
时,小球已经离开滑块,只受重力和绳的拉力,滑块对球的支持力为零,选项B正确;
C.当![]() 时,小球和楔形滑块一起加速,由整体法可知:
时,小球和楔形滑块一起加速,由整体法可知:
![]()
选项C错误;
D.当系统相对稳定后,竖直方向没有加速度,受力平衡,所以地面对A的支持力一定等于两个物体的重力之和,即
![]()
选项D正确。
故选BD。

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目