��Ŀ����
��ͼ��ʾ���ڹ⻬��Եˮƽ������ֱ������ϵxoy�����뾶ΪR=0.4m���ھ���С���ڱڹ⻬���ܱڼ�����Բ���ξ�Ե��ABˮƽ�̶��ڵڶ������ڣ�����A�˺�Բ�� ����y���ϣ�B����x���ϣ�
����y���ϣ�B����x���ϣ� ��y�Ḻ����нǦ�=60º��������ϵ�ĵ�һ��������ͬ�����ڴ������ĸ���ֱ��ˮƽ�����ǿ�ų��� a��b��cΪ�ų�������ֽ��ߣ����ǵ�ֱ�߷��̷ֱ�Ϊ
��y�Ḻ����нǦ�=60º��������ϵ�ĵ�һ��������ͬ�����ڴ������ĸ���ֱ��ˮƽ�����ǿ�ų��� a��b��cΪ�ų�������ֽ��ߣ����ǵ�ֱ�߷��̷ֱ�Ϊ ����a��b��Χ��������b��c��Χ��������ڵĴŸ�Ӧǿ�ȷֱ�Ϊ
����a��b��Χ��������b��c��Χ��������ڵĴŸ�Ӧǿ�ȷֱ�Ϊ ��
�� ����һ�����������������ڴŸ�Ӧǿ�Ⱦ�Ϊ
����һ�����������������ڴŸ�Ӧǿ�Ⱦ�Ϊ ����һ����m =1.2��10��5
����һ����m =1.2��10��5 �������q =1.0��10��6C��ֱ����С�ھ�Ե���ھ��Ĵ�����С���Ծ�Ե��A����v =2.0��10��2 m/s���ٶȴ�ֱy��������У����Ժ���˶������У�С���ܴ�ֱͨ��c��a���������Դ�ֱ��y����ٶȽ����Ե�ܶ����������˶�����
�������q =1.0��10��6C��ֱ����С�ھ�Ե���ھ��Ĵ�����С���Ծ�Ե��A����v =2.0��10��2 m/s���ٶȴ�ֱy��������У����Ժ���˶������У�С���ܴ�ֱͨ��c��a���������Դ�ֱ��y����ٶȽ����Ե�ܶ����������˶�����
��1�� �Ĵ�С�ͷ���
�Ĵ�С�ͷ���
��2�� ��
�� �Ĵ�С�ͷ���
�Ĵ�С�ͷ���
��3�����˶���һ�������ڣ�С���ھ�����һ�������Ĺ����У�����������˶���ʱ��������������˶���ʱ��֮�ȡ�
 ����y���ϣ�B����x���ϣ�
����y���ϣ�B����x���ϣ� ��y�Ḻ����нǦ�=60º��������ϵ�ĵ�һ��������ͬ�����ڴ������ĸ���ֱ��ˮƽ�����ǿ�ų��� a��b��cΪ�ų�������ֽ��ߣ����ǵ�ֱ�߷��̷ֱ�Ϊ
��y�Ḻ����нǦ�=60º��������ϵ�ĵ�һ��������ͬ�����ڴ������ĸ���ֱ��ˮƽ�����ǿ�ų��� a��b��cΪ�ų�������ֽ��ߣ����ǵ�ֱ�߷��̷ֱ�Ϊ ����a��b��Χ��������b��c��Χ��������ڵĴŸ�Ӧǿ�ȷֱ�Ϊ
����a��b��Χ��������b��c��Χ��������ڵĴŸ�Ӧǿ�ȷֱ�Ϊ ��
�� ����һ�����������������ڴŸ�Ӧǿ�Ⱦ�Ϊ
����һ�����������������ڴŸ�Ӧǿ�Ⱦ�Ϊ ����һ����m =1.2��10��5
����һ����m =1.2��10��5 �������q =1.0��10��6C��ֱ����С�ھ�Ե���ھ��Ĵ�����С���Ծ�Ե��A����v =2.0��10��2 m/s���ٶȴ�ֱy��������У����Ժ���˶������У�С���ܴ�ֱͨ��c��a���������Դ�ֱ��y����ٶȽ����Ե�ܶ����������˶�����
�������q =1.0��10��6C��ֱ����С�ھ�Ե���ھ��Ĵ�����С���Ծ�Ե��A����v =2.0��10��2 m/s���ٶȴ�ֱy��������У����Ժ���˶������У�С���ܴ�ֱͨ��c��a���������Դ�ֱ��y����ٶȽ����Ե�ܶ����������˶�������1��
 �Ĵ�С�ͷ���
�Ĵ�С�ͷ�����2��
 ��
�� �Ĵ�С�ͷ���
�Ĵ�С�ͷ�����3�����˶���һ�������ڣ�С���ھ�����һ�������Ĺ����У�����������˶���ʱ��������������˶���ʱ��֮�ȡ�

��1��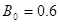 T ����ֱˮƽ�����£�2��
T ����ֱˮƽ�����£�2��
 ��3��
��3�� 
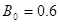 T ����ֱˮƽ�����£�2��
T ����ֱˮƽ�����£�2��
 ��3��
��3�� 
��1��С���ڵ�һ����a���뾶ΪR������Բ���˶�
��ţ�ٵڶ������У� ��2�֣�
��2�֣�
��ã� ��
��
�������ݵã�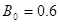 T ��2�֣�
T ��2�֣�
�����ֶ���֪ ����ֱˮƽ������.��2�֣�
����ֱˮƽ������.��2�֣�

��2��ҪʹС��ͣ�����������˶������������С���˶��İ뾶Ӧ��ȣ������ĴŸ�Ӧǿ��Ӧ�ȴ��� �ķ���Ϊ��ֱˮƽ�����£�
�ķ���Ϊ��ֱˮƽ�����£� �ķ���Ϊ��ֱˮƽ������ ��2�֣�
�ķ���Ϊ��ֱˮƽ������ ��2�֣�
С�����������˶��ľ�����ͼ��.
�����������С���Բ��Ϊ ��
�� ��С��Բ���˶��İ뾶Ϊ
��С��Բ���˶��İ뾶Ϊ ��ƫת��Ϊ
��ƫת��Ϊ ����ͼ����ʾ.
����ͼ����ʾ.
�ɼ���֪ʶ֪�� �ڣ�1�֣�
�ڣ�1�֣�

 �ۣ�1�֣�
�ۣ�1�֣�
 �ܣ�1�֣�
�ܣ�1�֣�
��ڢۢܵ� �ݣ�2�֣�
�ݣ�2�֣�
 ��2�֣�
��2�֣�
 �ޣ�1�֣�
�ޣ�1�֣�
��ܢݵ�
���У� ��2�֣�
��2�֣�
��3���� ֪��
֪��
С���ڵ�4����c��ǰ������Բ���˶�ʱ��Ϊ �ߣ�2�֣�
�ߣ�2�֣�
С��������������������Բ���˶�ʱ�乲Ϊ �ࣨ1�֣�
�ࣨ1�֣�
С���ڵ�1�������������������Բ���˶�ʱ��Ϊ �ᣨ1�֣�
�ᣨ1�֣�
�����˶���һ�������ڣ�С����ͨ����һ�������Ĺ����У�����������˶���ʱ�������������ʱ��֮��Ϊ ��
�� 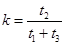 ��
��

��ţ�ٵڶ������У�
 ��2�֣�
��2�֣���ã�
 ��
���������ݵã�
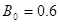 T ��2�֣�
T ��2�֣������ֶ���֪
 ����ֱˮƽ������.��2�֣�
����ֱˮƽ������.��2�֣�
��2��ҪʹС��ͣ�����������˶������������С���˶��İ뾶Ӧ��ȣ������ĴŸ�Ӧǿ��Ӧ�ȴ���
 �ķ���Ϊ��ֱˮƽ�����£�
�ķ���Ϊ��ֱˮƽ�����£� �ķ���Ϊ��ֱˮƽ������ ��2�֣�
�ķ���Ϊ��ֱˮƽ������ ��2�֣�С�����������˶��ľ�����ͼ��.
�����������С���Բ��Ϊ
 ��
�� ��С��Բ���˶��İ뾶Ϊ
��С��Բ���˶��İ뾶Ϊ ��ƫת��Ϊ
��ƫת��Ϊ ����ͼ����ʾ.
����ͼ����ʾ.�ɼ���֪ʶ֪��
 �ڣ�1�֣�
�ڣ�1�֣�
 �ۣ�1�֣�
�ۣ�1�֣� �ܣ�1�֣�
�ܣ�1�֣���ڢۢܵ�
 �ݣ�2�֣�
�ݣ�2�֣� ��2�֣�
��2�֣� �ޣ�1�֣�
�ޣ�1�֣���ܢݵ�

����
 ��2�֣�
��2�֣���3����
 ֪��
֪��С���ڵ�4����c��ǰ������Բ���˶�ʱ��Ϊ
 �ߣ�2�֣�
�ߣ�2�֣�С��������������������Բ���˶�ʱ�乲Ϊ
 �ࣨ1�֣�
�ࣨ1�֣�С���ڵ�1�������������������Բ���˶�ʱ��Ϊ
 �ᣨ1�֣�
�ᣨ1�֣������˶���һ�������ڣ�С����ͨ����һ�������Ĺ����У�����������˶���ʱ�������������ʱ��֮��Ϊ
 ��
�� 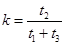 ��
����ݢޢߢ���� ��2�֣�
��2�֣�
 ��2�֣�
��2�֣�

��ϰ��ϵ�д�
�����Ŀ





 ����ֱ��MO��O������ų�����������ͨ��ֱ��MOʱ���ٶȷ����ƽ����PQ���������ӵ����������Ӽ�������������
����ֱ��MO��O������ų�����������ͨ��ֱ��MOʱ���ٶȷ����ƽ����PQ���������ӵ����������Ӽ�������������


 C��kg������ɴ�����Ϊ��0��-1����A�㴦�ɾ�ֹ�ͷţ������һ�����ٶȴ�����Ϊ��1��0����C���һ�ξ�x���������һ������һ��ʱ�䣬������ԭ��O�ٴλص��������
C��kg������ɴ�����Ϊ��0��-1����A�㴦�ɾ�ֹ�ͷţ������һ�����ٶȴ�����Ϊ��1��0����C���һ�ξ�x���������һ������һ��ʱ�䣬������ԭ��O�ٴλص��������
