题目内容
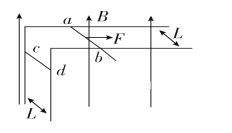
【题目】如右图所示，有一磁感应强度B＝9.1×10－4 T的匀强磁场，C、D为垂直于磁场的同一平面内的两点，它们之间的距离l＝0.05 m，今有一电子在此磁场中运动，它经过C点时的速度v的方向和磁场方向垂直，且与CD间的夹角α＝30°，问：
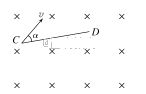
(1)电子在C点时所受的洛仑兹力的方向如何？
(2)若此电子在运动中后来又经过了D点，则它的速度v应是多大？
(3)电子从C点到D点所用的时间是多少？
(电子的质量m＝9.1×10－31 kg，电子的电量e＝1.6×10－19 C)
【答案】(1)垂直于v的方向斜向下 (2)8.0×106 m/s (3)6.5×10－9 s
【解析】
试题由题意知 C 、 D 为电子做匀速圆周运动的圆周轨迹上的两点，故 C 、 D 两点的速度大小相同,若根据几何关系求出 CD 弧长所对的圆心角∠ COD ，如图，就可以利用 CD 弦长求出 R ，进而求得速度 v 。
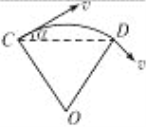
(1) 由左手定则，判断出洛仑兹力的方向为垂直于v的方向斜向下；
(2)由
，解得
，∠ DCO =90°－α=60°，故△ OCD 为正三角形，
， 
；
(3)
；
练习册系列答案
相关题目
