题目内容
 如图,一条长为L的细线上端固定,下端拴一个质量为m的带电为q的小球,将它置于一方向水平向右的匀强电场中,使细线竖直拉直时小球在A点静止释放,当细线离开竖直位置偏角α=60°时,小球速度为0.
如图,一条长为L的细线上端固定,下端拴一个质量为m的带电为q的小球,将它置于一方向水平向右的匀强电场中,使细线竖直拉直时小球在A点静止释放,当细线离开竖直位置偏角α=60°时,小球速度为0.(1)求:①小球带电性质②电场强度E.
(2)要小球恰好完成竖直圆周运动,求A点释放小球时应有初速度vA.(可含根式)
分析:(1)小球在电场中受到重力、电场力和细线的拉力而处于平衡状态.根据细线偏离的方向,分析电场力方向,确定小球的电性.根据平衡条件和电场力公式F=qE,列方程求出电场强度.
(2)根据题意可知,由力的平行四边形定则求出电场力与重力的合力,可等效成新的重力,小球若能以最小速度通过新重力的对应的最高点,则小球恰好完成竖直圆周运动,从而根据动能定理,可求出A点释放小球时应有初速度的大小.
(2)根据题意可知,由力的平行四边形定则求出电场力与重力的合力,可等效成新的重力,小球若能以最小速度通过新重力的对应的最高点,则小球恰好完成竖直圆周运动,从而根据动能定理,可求出A点释放小球时应有初速度的大小.
解答:解:(1)由图可知,小球所受电场力方向水平向右,场强也水平向右,则小球带正电荷.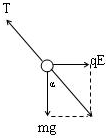
由题意可知,细线离开竖直位置偏角的角平分线的位置,即为小球平衡位置,
以小球为研究对象,分析受力,作出受力示意图如图.根据平衡条件得:
qE=mgtan
则:E=
=
;
(2)小球除拉力外,还受到电场力与重力作用,由于其两个不变,因此可等效成新的重力,所以要小球恰好完成竖直圆周运动,则小球必须能以最小速度通过新的重力对应的最高点.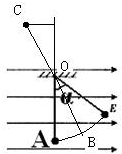
根据牛顿第二定律,则有:
=
mg=m
;
从而A点到新的重力对应的最高点C,根据动能定理得,
-mgL(1+cos30°)-qELsin60°=
mvC2-
mvA2;
qE=
mg
联立两式解得,vA=
.
答:(1)小球带正电,电场强度为
;
(2)细线摆到竖直位置时,小球的速度为
.

由题意可知,细线离开竖直位置偏角的角平分线的位置,即为小球平衡位置,
以小球为研究对象,分析受力,作出受力示意图如图.根据平衡条件得:
qE=mgtan
| α |
| 2 |
则:E=
| mgtan30° |
| q |
| ||
| 3q |
(2)小球除拉力外,还受到电场力与重力作用,由于其两个不变,因此可等效成新的重力,所以要小球恰好完成竖直圆周运动,则小球必须能以最小速度通过新的重力对应的最高点.

根据牛顿第二定律,则有:
| (mg)2+(qE)2 |
2
| ||
| 3 |
| ||
| L |
从而A点到新的重力对应的最高点C,根据动能定理得,
-mgL(1+cos30°)-qELsin60°=
| 1 |
| 2 |
| 1 |
| 2 |
qE=
| ||
| 3 |
联立两式解得,vA=
(2+2
|
答:(1)小球带正电,电场强度为
| ||
| 3q |
(2)细线摆到竖直位置时,小球的速度为
(2+2
|
点评:本题整合了物体的平衡、牛顿第二定律和动能定理等多个规律,分析受力是基础,要培养分析受力情况、作力图的习惯,注意不是小球能通过几何最高点,就能恰好做完整的圆周运动,这是解题的关键之处,也是重难点,同时掌握等效重力的方法.

练习册系列答案
相关题目
 如图,一条长为L 的细线,上端固定,下端拴一质量为m的带电小球.将它置于一电场强度大小为E、方向水平的匀强电场中.已知当细线离开竖直线的偏角为α=30°时,小球处于平衡,问:
如图,一条长为L 的细线,上端固定,下端拴一质量为m的带电小球.将它置于一电场强度大小为E、方向水平的匀强电场中.已知当细线离开竖直线的偏角为α=30°时,小球处于平衡,问: 如图,一条长为l的细线,上端固定,下端拴一质量为m的带电小球.将它置于一匀强电场中,电场强度大小为E,方向是水平的.已知当细线离开竖直位置的偏角为α=300时,小球处于平衡.
如图,一条长为l的细线,上端固定,下端拴一质量为m的带电小球.将它置于一匀强电场中,电场强度大小为E,方向是水平的.已知当细线离开竖直位置的偏角为α=300时,小球处于平衡.
