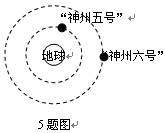
题目内容
将火星和地球绕太阳的运动近似看成是同一平面内的同方向绕行的匀速圆周运动,已知火星的轨道半径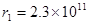 m,地球的轨道半径为
m,地球的轨道半径为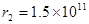 m,根据你所掌握的物理和天文知识,估算出火星与地球相邻两次距离最小的时间间隔为 ( )
m,根据你所掌握的物理和天文知识,估算出火星与地球相邻两次距离最小的时间间隔为 ( )
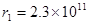 m,地球的轨道半径为
m,地球的轨道半径为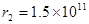 m,根据你所掌握的物理和天文知识,估算出火星与地球相邻两次距离最小的时间间隔为 ( )
m,根据你所掌握的物理和天文知识,估算出火星与地球相邻两次距离最小的时间间隔为 ( )| A.1年 | B.2年 | C.3年 | D.4年 |
B
因为火星的轨道半径大于地球的轨道半径,由 r^3 / T^2=K (开普勒第三定律)可知,火星的公转周期较大。火星与地球相距最近,意思是说两者在太阳同一侧的同一条“轨道半径”上。,设火星再次与地球相距最近需要的时间是 t ,则:ω地* t -ω火* t=2π(地球转过的角度与火星转过的角度刚好相差2π 弧度),即:2π t [ ( 1 / T地)-( 1 / T火) ]=2π
得所求时间是 t=T地*T火 /(T火-T地),而r1^3 / T火^2=r2^3 / T地^2,即:T火 / T地=( r1 / r2 )^(3/2)=( 2.3 / 1.5 )^(3/2)=(23 / 15) ^(3/2)=1.9,得:火星公转周期是T火=1.9年(因为 T地=1年)。所以,t=1*1.9 / (1.9-1)=2.11年。B正确。故本题选B。
得所求时间是 t=T地*T火 /(T火-T地),而r1^3 / T火^2=r2^3 / T地^2,即:T火 / T地=( r1 / r2 )^(3/2)=( 2.3 / 1.5 )^(3/2)=(23 / 15) ^(3/2)=1.9,得:火星公转周期是T火=1.9年(因为 T地=1年)。所以,t=1*1.9 / (1.9-1)=2.11年。B正确。故本题选B。

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 .已知地球半径为R,地面重力加速度为
.已知地球半径为R,地面重力加速度为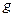 .求这颗卫星运转的线速度大小和周期分别是多少?
.求这颗卫星运转的线速度大小和周期分别是多少?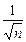 (
( >1),那么该卫星离地面的高度是地球半径的
>1),那么该卫星离地面的高度是地球半径的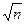 倍
倍