Question

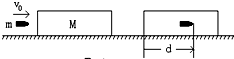如图所示，在光滑的水平地面上静止着质量为M的木块，一粒质量为m初速为v₀的子弹水平击中木块，打入深度为d，试求转化为内能的值△E是多少？

Answer 1

分析：以子弹和木组成的系统为研究对象，子弹水平击中木块过程，动量守恒．根据动量守恒定律求出子弹水平击中木块后的速度．系统动能的减小转化为内能，再由能量守恒定律求出内能△E．

解答：解：由题，以子弹和木组成的系统为研究对象，水平面光滑，系统动量守恒，以子弹初速度方向为正方向，得到
     mv₀=（m+M）V，得V=

mv0

M+m

子弹和木块发生的是完全非弹性碰撞，损失的动能最多，通过内力做负功转化为系统的内能为：△E=f?d=

1

2

m

v

2 0

-

1

2

(m+M)V2=

M

m+M

?

1

2

m

v

2 0

=

Mm v 2 0

2(M+m)

答：转化为内能的值△E是

Mm v 2 0

2(M+m)

．

点评：子弹打击木块与碰撞相似，遵守两大守恒定律：动量守恒定律和能量守恒定律．基本题，不容有失．