题目内容
设月球绕地球运动是一个圆轨道，已知地球半径R，月球的质量为m，它到地球表面的距离为h，地面上的重力加速度为g，根据这些物理量不能知道．（ ）A．月球绕地球运动的速度
B．月球表面的重力加速度
C．月球绕地球运动的周期
D．月球绕地球运动的动能
【答案】分析：月球绕地球做匀速圆周运动，由地球的万有引力提供向心力，列式可求出月球的速度v；由T=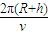
，可求得周期；由Ek=
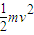可求出月球绕地球运动的动能．
解答：解：A、月球绕地球做匀速圆周运动，由地球的万有引力提供向心力，则有
G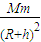
=m
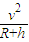
得月球绕地球运动的速度v=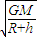
，M、R、h已知，G是常量，所以月球绕地球运动的速度v可以求出，故A错误．
B、月球表面的重力加速度无法求出．故B正确．
C、月球绕地球运动的周期T=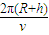
，可见，T可求出．故C错误．
D、月球绕地球运动的动能Ek=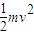
，则知Ek可求出．故D错误．
故选B
点评：本题关键要建立物理模型，抓住万有引力提供月球的向心力，结合圆周运动的公式，即可得到解答．
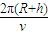，可求得周期；由Ek=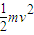可求出月球绕地球运动的动能．解答：解：A、月球绕地球做匀速圆周运动，由地球的万有引力提供向心力，则有
G
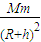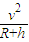
=m得月球绕地球运动的速度v=
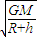，M、R、h已知，G是常量，所以月球绕地球运动的速度v可以求出，故A错误．B、月球表面的重力加速度无法求出．故B正确．
C、月球绕地球运动的周期T=
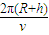，可见，T可求出．故C错误．D、月球绕地球运动的动能Ek=
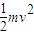，则知Ek可求出．故D错误．故选B
点评：本题关键要建立物理模型，抓住万有引力提供月球的向心力，结合圆周运动的公式，即可得到解答．
练习册系列答案
唐印文化课时测评系列答案
导学与测试系列答案
相关题目
，月球的半径R2约为月球与地球距离R1的
，月球绕地球运动（看作圆周运动）的平均速率为v1=1.0km/s。“嫦娥1号”安装的太阳能电池帆板的面积S=8πm2。该太阳能电池将太阳能转化为电能的转化率η=11%。已知太阳辐射的总功率为P0=3.8×1026 W。月球与太阳之间的平均距离R=1.5×1011 m。估算（结果取2位有效数字）
，k是一个对所有行星都相同的常量。将行星绕太阳的运动按圆周运动处理，请你推导出太阳系中该常量k的表达式。已知引力常量为G，太阳的质量为M太。
①
②
③
④
如图所示，在以坐标原点O为圆心、半径为R的半圆形区域内，有相互垂直的匀强电场和匀强磁场，磁感应强度为B，磁场方向垂直于xOy平面向里。一带正电的粒子（不计重力）从O点沿y轴正方向以某一速度射入，带电粒子恰好做匀速直线运动，经t0时间从P点射出。
时间恰从半圆形区域的边界射出。求粒子运动加速度的大小。