题目内容

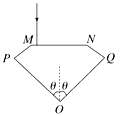
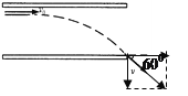
【题目】用半径相同的两小球A、B的碰撞验证动量守恒定律，实验装置示意如图，斜槽与水平槽圆滑连接。实验时先不放B球，使A球从斜槽上某一固定点 C由静止滚下，落到位于水平地面的记录纸上留下痕迹。再把B求静置于水平槽前端边缘处，让 A球仍从 C处由静止滚下，A球和 B球碰撞后分别落在记录纸上留下各自的痕迹。记录纸上的 O点是垂直所指的位置，若测得各落点痕迹到 O点的距离：OM=2.68cm，OP=8.62cm，ON=11.50cm，并知 A、B两球的质量比为 2：1，则未放 B球时 A球落地点是记录纸上的____点，系统碰撞前总动量 P与碰撞后总动量的百分误差=_______％（结果保留一位有效数字）。

【答案】p 2%

【解析】试题分析：A球从固定点C由静止滚下，滚到最低点时有相同的水平速度v0，而A、B两球平抛后，下不落高度h相同，由h=知，运动时间t相同.水平方向v=.故小球的动量与水平位移成正比.若mAxA与（mAxA′+mBxB′）基本相等，则碰撞前后动量守恒.

碰后A的速度会变小，故p点是未放B球时A球落地的.

p=mA｜Op｜=mA×8.62 cm

p′=mA｜OM｜+mA｜ON｜=mA×8.62 cm+mB×11.50 cm=mA×8.43 cm

故=0.198.62=0.02.=2%.

练习册系列答案
相关题目

【题目】打磨某剖面如图所示的宝石时，必须将OP、OQ边与轴线的夹角θ切磨在θ1<θ<θ2的范围内，才能使从MN边垂直入射的光线，在OP边和OQ边都发生全反射(仅考虑如图所示的光线第一次射到OP边并反射到OQ边后射向MN边的情况)，则下列判断正确的是(　　)

A. 若θ>θ2，光线一定在OP边发生全反射

B. 若θ>θ2，光线会从OQ边射出

C. 若θ<θ1，光线会从OP边射出

D. 若θ<θ1，光线会在OP边发生全反射

【题目】平衡位置处于坐标原点的波源S在y轴上振动，产生频率为50 Hz的简谐横波向x轴正、负两个方向传播，波速均为100 m/s.平衡位置在x轴上的P、Q两个质点随波源振动着，P、Q的x轴坐标分别为xP＝3.5 m、xQ＝－3 m．当S位移为负且向－y方向运动时，P、Q两质点的( )

A. 位移方向相同、速度方向相反

B. 位移方向相同、速度方向相同

C. 位移方向相反、速度方向相反

D. 位移方向相反、速度方向相同

【题目】如图所示，绝热气缸封闭一定质量的理想气体，气缸内壁光滑，有一绝热活塞可在气缸内自由滑动，活塞的重力为500 N、横截面积为100 cm2。当两部分气体的温度都为27 ℃时，活塞刚好将缸内气体分成体积相等的A、B上下两部分，此时A气体的压强为p0＝105 Pa，现把气缸倒置，仍要使两部分体积相等，则需要把A部分的气体加热到多少摄氏度？

【题目】在同一地点有两个静止的声源，发出声波1和声波2．在同一空间的空气中沿同一方向传播，如图所示为某时刻这两列波的图象，则下列说法中正确的是（ ）

A. 波1速度比波2速度大

B. 在这两列波传播的方向上运动的观察者，听到的这两列波的频率可以相同

C. 在这两列波传播的方向上，会产生稳定的干涉现象

D. 相对于同一障碍物，波1比波2更容易发生衍射现象

【题目】汽车关闭发动机后恰能沿斜坡匀速下滑，在这过程中正确的说法（ ）

A. 汽车机械能守恒 B. 汽车的动能和势能相互转化

C. 机械能逐渐转化为内能，总能量守恒 D. 机械能和内能之间没有转化

【题目】如图所示，一束截面为圆形(半径R=1 m)的平行紫光垂直射向一半径也为R的玻璃半球的平面，经折射后在屏幕S上形成一个圆形亮区。屏幕S至球心的距离为D=(＋1) m，不考虑光的干涉和衍射，试问：

(1)若玻璃半球对紫色光的折射率为n=，请你求出圆形亮区的半径。

(2)若将题干中紫光改为白光，在屏幕S上形成的圆形亮区的边缘是什么颜色？

【题目】如图平行金属板长为L，一个带电为+q，质量为m的粒子以初速度v0紧贴上板垂直射入电场，刚好从下板边缘射出，末速度恰与下板成60O角，粒子重力不计。求：

（1）粒子末速度大小.

（2）电场强度.

（3）两极间距离d.

【题目】如图所示,一物块P质量m=2 kg,由平面上A点开始以速度v0=4 m/s向A点右侧运动,物块与平面之间的动摩擦因数μ1=0.2,运动x1=3 m 后滑上传送带BC。已知传送带足够长且物块与传送带之间的动摩擦因数μ2=0.1,传送带以恒定速率v2=1 m/s逆时针转动。(g取 10 m/s2)求:

(1)物块向右运动距A点的最大距离;

(2)物块最后停下来时距A点的距离。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网