题目内容
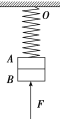
【题目】如图所示，悬挂于O点的轻质弹簧，劲度系数k＝100 N/m，其下端拴一质量m＝1 kg的小物体A，紧挨物体A有一质量M＝2 kg的物体B，现对B施加一个竖直向上、大小为38 N的力F，系统处于静止状态，现突然改变力F的大小，使物体A、B以加速度a＝2 m/s2匀加速下降，直到A、B两物体分离，取g＝10 m/s2，则（ ）
A.两物体刚开始匀加速下降时，力F大小为8 N
B.两物体分离时，弹簧刚好恢复原长
C.改变力F的大小后经0.4 s ,A、B两物体分离
D.从改变力F到两物体分离的过程中，系统克服力F做的功为3.84 J
【答案】CD
【解析】
A.系统静止时，弹簧处于压缩状态，令压缩量为x1，则
，
代入数据得
，
A、B两物体刚开始匀加速下降时有
，
代入数据得
故A错误；
B.设经时间t两物体分离，A、B间的弹力为0，弹簧处于拉伸状态，令拉伸量为x2，则对A有
，
代入数据得
，
故B错误；
C.A、B分离时A、B两物体组成的系统下降的距离为
，
而
，
代入数据得
，
故C正确；
D.因刚开始和两物体分离时，弹簧的形变量一样，整个过程弹簧弹力做功为零，由动能定理知
，
联立
并代入数据得
，
故D正确；
练习册系列答案
名校课堂系列答案
相关题目
