题目内容
在光滑的水平面上有一质量为2kg的物体，它的左端与一劲度系数为l00N/m的轻弹簧相连，右端连接一细线，物体静止时细线与竖直方向成37°角，此时水平面对物体的弹力为零，如图所示．已知sin37°=0.6，cos37°=0.8，重力加速度g取10m/s2，则下列说法正确的是（ ）分析：以物体为研究对象，进行受力分析，抓住剪断弹簧的瞬间，细线的拉力会突变，而剪断细线的瞬间，弹簧的弹力不突变，根据牛顿第二定律进行求解．
解答：解：A、B以物体为研究对象，进行受力分析可知，物体受细线拉力为T=25N，弹簧弹力为F=15N，在剪断弹簧的瞬间，细线的拉力会突变，物体静止不动，细线的拉力为0，加速度为0，故AB错误．
C、D在剪断细线的瞬间，弹簧的弹力不突变，受力分析可知，此时物体受到的合外力为15N，根据牛顿第二定律得：加速度为a=
=7.5m/s2．故C错误，D正确．
故选D
C、D在剪断细线的瞬间，弹簧的弹力不突变，受力分析可知，此时物体受到的合外力为15N，根据牛顿第二定律得：加速度为a=
| F合 |
| m |
故选D
点评：本题的解题关键是抓住弹簧与细线模型的不同，根据不同的特点分析瞬间小球的受力情况，由牛顿第二定律求解．
练习册系列答案
相关题目
在光滑的水平面上有一直角坐标系，现有一个质量m=0.1kg的小球，从y轴正半轴上的P1点以速度v0=0.6m/s垂直于y轴射入．已知小球在y＞0的空间内受到一个恒力F1的作用，方向沿y轴负方向，在y＜0的空间内小球受到一平行于水平面、大小不变F2的作用，且F2的方向与小球的速度方向始终垂直．现小球从P1点进入坐标系后，经x=1.2m的P2点与x轴正方向成53°角射入y＜0的空间，最后从y轴负半轴上的P3点垂直于y轴射出．如图所示，（已知：sin53°=0.8，cos53°=0.6）．求：
B．如图所示，在光滑的水平面上有一长L=1m的钢槽A，槽中有一物体B，A和B的质量相同，AB间的动摩擦因数μ=0.05．开始时B位于钢槽的中央，都处于静止状态．现给一个瞬时速度υ0=5m/s，使它向右运动．如果B与A两侧的挡板相碰撞是无动能损耗，则B与A的左右两挡板最多能相碰
（2005?宿迁模拟）如图所示在光滑的水平面上有一平板小车M正以速度v向右运动．现将一质量为m的木块无初速度放上小车，由于木块和小车间的摩擦力作用，小车的速度将发生变化．为使小车保持原来的运动速度不变，必须及时对小车施加一向右的水平恒力F．当F作用一段时间后把它撤去时，木块恰能随小车一起以速度v共同向右运动．设木块和小车间的动摩擦因素为μ，求在上述过程中，水平恒力F对小车做多少功？
（2012?无锡二模）如图所示，在光滑的水平面上有一直角坐标系Oxy．现有一个质量m=O．lkg．带电荷量q=一2×10-4C的微粒，从y轴正半轴上的P1点以速度v0=0.6m/s垂直于y轴射入．已知在y＞0的空间内有与y轴方向平行的匀强电场，在y＜0的空间内存在方向与纸面垂直的匀强磁场．带电微粒从P1点射入电场后，经坐标（1.2，0）的P2点与x轴正方向成53°角射入y＜0的空间，最后从y轴负半轴上的P3点垂直于y轴射出．（已知：sin53=0.8，cos53°=0.6）求：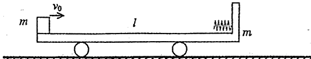
如图所示，在光滑的水平面上有一质量为m，长度为l的小车，小车左端有一质量也是m可视为质点的物块．车子的右壁固定有一个处于锁定状态的压缩轻弹簧（弹簧长度与车长相比可忽略），物块与小车间动摩擦因数为μ，整个系统处于静止．现在给物块一个水平向右的初速度v0，物块刚好能与小车右壁的弹簧接触，此时弹簧锁定瞬间解除，当物块再回到左端时，与小车相对静止．求：