题目内容
如图所示,1,2两木块用短钩相连,放在水平地面上,1和2两木块的质量分别是m1=1 kg和m2=2kg,它们与水平地面间的动摩擦因数均为μ=0.1。在t=0时开始用向右的水平恒力F=6 N拉木块2,使两木块—起运动,过一段时间后短钩脱开。当木块2的速度v2=8m/s时,1,2两木块相距S=13m,此时木块1已停下一段时间,若不计短钩的长度,g取10m/s2。求
(1)短钩脱外瞬间两木块的速度v1的大小。
(2)从t=0外始经过多长时间短钩脱开?
解:设脱钩前两木块运动的加速为a
a=![]() =1 m/s2 设脱钩后,木块1的加速为a1,木块2的加速度为a2,则a1=
=1 m/s2 设脱钩后,木块1的加速为a1,木块2的加速度为a2,则a1=![]() =μg=1m/s2 ,a2=
=μg=1m/s2 ,a2=![]() =2m/s2 ,设经时间t短钩脱开v1=at ,v12=2a1s1 v22-v12=2a2s2 s2-s1=s 由以上四式解得v1=2 m/s t=2s
=2m/s2 ,设经时间t短钩脱开v1=at ,v12=2a1s1 v22-v12=2a2s2 s2-s1=s 由以上四式解得v1=2 m/s t=2s
【解析】此题为两个物体构成的系统,对牛顿第二定律及运动学规律进行了考查。正确的选取研究对象并进行受力分析,找出两个物体位移之间的几何关系是解决此题的关键。

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案
相关题目
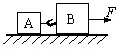 如图所示,1、2木块用短钩相连,放在水平地面上.1和2两木与块的质量分别为m1=1.0千克和m2=2.0千克.它们与水平地面间的摩擦系数均为μ=0.10.在t=0秒时开始用向右的水平恒力F=6.0牛拉木块2.过一段时间后短钩脱开.到t=6.0秒时1、2两木块相距S=18.0米,此时木块1早已停住.求此时木块2的速度.
如图所示,1、2木块用短钩相连,放在水平地面上.1和2两木与块的质量分别为m1=1.0千克和m2=2.0千克.它们与水平地面间的摩擦系数均为μ=0.10.在t=0秒时开始用向右的水平恒力F=6.0牛拉木块2.过一段时间后短钩脱开.到t=6.0秒时1、2两木块相距S=18.0米,此时木块1早已停住.求此时木块2的速度.

 木匠用质量为m0的钉锤击打质量为m(m0≥m)的钉子,把木条钉牢在竖直的木墙上.在钉人某一颗钉子时,测得第一次敲打使钉子进入的深度为L,如图所示.
木匠用质量为m0的钉锤击打质量为m(m0≥m)的钉子,把木条钉牢在竖直的木墙上.在钉人某一颗钉子时,测得第一次敲打使钉子进入的深度为L,如图所示.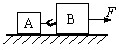 如图所示,1、2木块用短钩相连,放在水平地面上.1和2两木与块的质量分别为m1=1.0千克和m2=2.0千克.它们与水平地面间的摩擦系数均为μ=0.10.在t=0秒时开始用向右的水平恒力F=6.0牛拉木块2.过一段时间后短钩脱开.到t=6.0秒时1、2两木块相距S=18.0米,此时木块1早已停住.求此时木块2的速度.
如图所示,1、2木块用短钩相连,放在水平地面上.1和2两木与块的质量分别为m1=1.0千克和m2=2.0千克.它们与水平地面间的摩擦系数均为μ=0.10.在t=0秒时开始用向右的水平恒力F=6.0牛拉木块2.过一段时间后短钩脱开.到t=6.0秒时1、2两木块相距S=18.0米,此时木块1早已停住.求此时木块2的速度.