题目内容
【题目】如图所示，在一端封闭的光滑细玻璃管中注满清水，水中放一红蜡块R（R视为质点）．将玻璃管的开口端用胶塞塞紧后竖直倒置且与y轴重合，在R从坐标原点以速度v0=3cm/s匀速上浮的同时，玻璃管沿x轴正向做初速度为零的匀加速直线运动，合速度的方向与y轴夹角为α．则红蜡块R的（ ）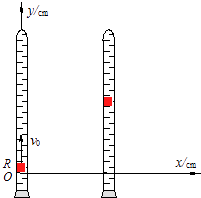
A.分位移y与x成正比
B.分位移y的平方与x成正比
C.合速度v的大小与时间t成正比
D.tanα与时间t成正比
【答案】B,D
【解析】解：A、由题意可知，y轴方向，y=v0t；
而x轴方向，x= 
，联立可得：x= 
，故A错误，B正确；
C、x轴方向，vx=at，那么合速度的大小v= 
，则v的大小与时间t不成正比，故C错误；
D、设合速度的方向与y轴夹角为α，则有： 
，故D正确；
故选：BD．
小圆柱体红蜡快同时参与两个运动：y轴方向的匀速直线运动，x轴方向的初速为零的匀加速直线运动．根据位移与时间表达式，从而确定分位移y与x的关系，再由y方向可求运动时间，接着由x方向求加速度，从而求得vx，再由速度合成求此时的速度大小，最后由两方向的速度关系，可知tanα与时间t的关系．
练习册系列答案
相关题目
