如图所示.光滑曲面AB与水平地面BC相切于B.竖直光滑半圆轨道CD与水平地面BC切于C.已知圆轨道半径为R.BC长为4R.且表面粗糙.一滑块从AB轨道上距地面4R高度处由静止释放.之后能够通过圆轨道的最高点D.且对D处的压力为0.求:(1)若从曲面上距地2R高度处无初速释放滑块.滑块将停在何处,(2)若使滑块通过D处后水平抛出.刚好击中地面上的B点.应从AB轨道上离地题目和参考答案——青夏教育精英家教网—

题目内容

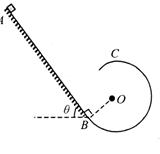
（12分）如图所示，光滑曲面AB与水平地面BC相切于B，竖直光滑半圆轨道CD与水平地面BC切于C，已知圆轨道半径为R，BC长为4R，且表面粗糙，一滑块从AB轨道上距地面4R高度处由静止释放，之后能够通过圆轨道的最高点D，且对D处的压力为0，求：

（1）若从曲面上距地2R高度处无初速释放滑块，滑块将停在何处；
（2）若使滑块通过D处后水平抛出，刚好击中地面上的B点，应从AB轨道上离地面多高处由静止释放滑块．

(1) 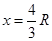(2)

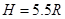
解析试题分析：(1)从高4R处释放恰能过最高点D，设动摩擦因数为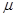，由动能定理知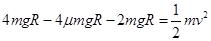：  ① 在D点，有 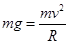②
从2R处释放后滑块将运动到圆周上h高处，则有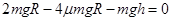 ③
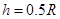解得： ④
滑块将沿水平轨道向左滑动距离x减速至零，有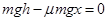 ⑤
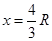解得： ⑥
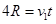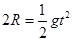(2)要使滑块击中B点，则从D点平抛的速度为v₁，满足 ⑦  且 ⑧
由释放到运动到D点过程中，有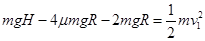 ⑨
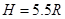解得：  ⑩
考点：本题综合考查了向心力公式、平抛运动规律和动能定理的应用，关键要明确运动过程中每一段的运动性质，选择合适的规律求解，其次要理解“通过D点时的压力为零”的含义是重力恰好提供向心力．

练习册系列答案

中考分类必备全国中考真题分类汇编系列答案

相关题目

如图所示，已知半径分别为R和r的甲、乙两个光滑的圆形轨道安置在同一竖直平面上，甲轨道左侧又连接一个光滑的轨道，两圆形轨道之间由一条水平轨道CD相连．一小球自某一高度由静止滑下，先滑上甲轨道，通过动摩擦因数为μ的CD段，又滑上乙轨道，最后离开两圆轨道．若小球在两圆轨道的最高点对轨道压力都恰好为零．试求：⑴分别经过C、D时的速度； ⑵小球释放的高度h； ⑶水平CD段的长度．

（10分）如图所示，AB和CDO都是处于竖直平面内的光滑圆弧形轨道，OA处于水平位置。AB是半径为R＝2m的1／4圆周轨道，CDO是半径为r＝1m的半圆轨道，最高点O处固定一个竖直弹性档板。D为CDO轨道的中央点。BC段是水平粗糙轨道，与圆弧形轨道平滑连接。已知BC段水平轨道长L＝2m，与小球之间的动摩擦因数μ＝0．4。现让一个质量为m＝1kg的小球P从A点的正上方距水平线OA高H处自由落下。（取g＝10m／s²）

（1）当H＝1．4m时，问此球第一次到达D点对轨道的压力大小。
（2）当H＝1．4m时，试通过计算判断此球是否会脱离CDO轨道。如果会脱离轨道，求脱离前球在水平轨道经过的路程。如果不会脱离轨道，求静止前球在水平轨道经过的路程。

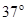（16分）滑雪是人们喜爱的一项体育运动．一滑雪坡由AB和BC组成，AB是倾角为的斜坡，BC是半径为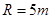的圆弧面，圆弧面和斜面相切于B，与水平面相切于C，如图所示，AB竖直高度差为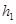，竖直台阶CD高度差为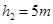，台阶底端与倾角为斜坡DE相连．运动员连同滑雪装备总质量为80kg，从A点由静止滑下以，通过C点后飞落到DE上（不计空气阻力和轨道的摩擦阻力，取10m/s²，sin37°=0.6，cos37°=0.8）．求：

（1）AB竖直方向的高度差；
（2）运动员刚过B点瞬间轨道受到的压力？
（3）运动员在空中飞行的时间？

（8分）如图甲所示，固定在水平面上电阻不计的光滑金属导轨，间距d＝0.5m，导轨右端连接一阻值为R＝4Ω的小灯泡L.在CDEF矩形区域内有竖直向上的匀强磁场，磁感应强度B随时间t变化如图乙所示，CF长为2m.在t＝0时刻，电阻为r=1Ω的金属棒ab在水平恒力F=0.2N作用下，由静止开始沿导轨向右运动,t＝4s时进入磁场，并恰好能够匀速运动。求：

（1）0-4s内通过小灯泡的电流强度；
（2）金属棒在磁场中匀速运动的速度；
（3）金属棒的质量。

（12分）如图所示，质量M＝400g的劈形木块B上叠放一木块A，A的质量为m＝200g。A、B一起放在斜面上，斜面倾角θ＝37°，B的上表面呈水平，B与斜面之间及B与A之间的动摩擦因数均为μ＝0.2。当B受到一个F＝5.76N的沿斜面向上的作用力时，A相对B静止，并一起沿斜面向上运动。
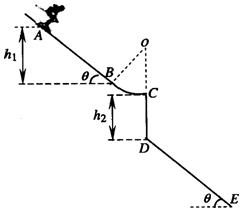
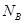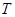（sin37°＝0.6，cos37°＝0.8，g＝10m/s2）

求：（1）B的加速度大小；
（2）A受到的摩擦力及A对B的压力大小。

(11分)如图甲所示，质量为m＝1kg的物体置于倾角为θ＝37°的固定斜面上（斜面足够长），对物体施加平行于斜面向上的恒力F，作用时间t₁＝1s时撤去拉力，物体运动的部分v—t图像如图乙所示，取g=10m/s²，试求：

（1）拉力F的大小和斜面的动摩擦因数；
（2）求拉力F对物体所做的功

(15 分）如图，是一段光滑的固定斜面，长度s=1m，与水平面的倾角θ=53⁰。另有一固定竖直放置的粗糙圆弧形轨道刚好在B点与斜面相切，圆弧形轨道半径R=0.3m，O点是圆弧轨道的圆心。将一质量m=0.2kg的小物块从A点由静止释放，运动到圆弧轨道最高点C点时，与轨道之间的弹力F=1N。重力加速度g=10m/s²,sin53?=0.8,cos53?=0.6，不计空气阻力。求：

(1)小物块运动到B点时的速度大小？
(2)小物块从B到C的过程，克服摩擦力做的功是多少？

试题分类