Question

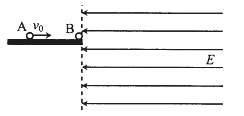
【题目】如图所示，为车站使用的水平传送带装置模型，绷紧的传送带水平部分AB的长度L＝5m，并以v＝2m/s的速度向右运动。现将一个可视为质点的旅行包轻轻地无初速地放在传送带的A端，已知旅行包与皮带之间的动摩擦因数μ＝0.2，g＝10m/s2。求：

（1）旅行包在传送带上从A端运动到B端所用的时间t；

（2）旅行包在传送带上相对滑动时留下的痕迹的长度s。

Answer 1

【答案】（1）3s（2）1m

【解析】试题分析：（1）旅行包无初速度地轻放在传送带的左端，在传送带上先做匀加速直线运动，达到传送带速度后做匀速直线运动，根据牛顿第二定律结合运动学公式求出运动的总时间．

（2）求出该时间内物体的位移，由平均速度公式求出传送带的位移，最后求出痕迹的长度．

解：（1）设旅行包在传送带上匀加速运动t1后达到与传送带共速，发生的位移为x，

由牛顿第二定律得：f=ma ①

f=μmg ②

v=at1③

④

解得：x=1m＜5m，所以物体先做匀加速直线运动，后做匀速直线运动．

设匀速直线运动时间t2，则：L﹣x=vt2⑤

t=t1+t2⑥

联立解得：t=3s ⑦

（2）旅行包相对滑动过程传送带位移为：x'=vt1⑧

旅行包相对滑动时留下的痕迹的长度：s=x'﹣x ⑨

联立解得：s=1m

答：（1）旅行包在传送带上从A端运动到B端所用的时间t为3s；

（2）旅行包在传送带上相对滑动时留下的痕迹的长度s为1m．