题目内容
【题目】假设宇宙中存在一些离其它恒星较远的、由质量相等的四颗星组成的四星系统，设其它星体对它们的引力作用可忽略．已知稳定的四星系统存在两种基本的构成形式，一种形式是三颗星位于等边三角形的三个顶点上，第四颗位于其中心，并沿外接于等边三角形的圆形轨道运行；另一种形式是四颗星位于正方形的四个顶点上，围绕正方形的中心做圆轨道运行．设每颗星体的质量均为m，它们做圆周运动的半径为R，试分别求出这两种情况下四星系统的运动周期T1和T2.(已知万有引力常量为G)
【答案】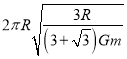
； 
；
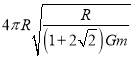【解析】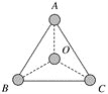
第一种情况，O对A的作用力为： 
设A、C距离为r，则：r＝2Rcos 30°
C对A的作用力为：
B、C对A的合力为：F2＝2F′cos 30°＝
故对A有：F1＋F2＝
联立解得：T1＝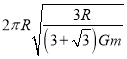
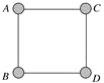
第二种情况，D对A的作用力为：F1＝
C对A的作用力为： 
B、C对A的合力为
故对A有：F1＋F2＝
联立解得：T2＝4πR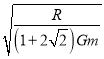
练习册系列答案
导学全程练创优训练系列答案
相关题目
