题目内容
 小车以某一初速沿水平长木板向左作匀减速运动,
小车以某一初速沿水平长木板向左作匀减速运动,长木板左端外有一传感器,通过数据采集器和计算
机相连,可测得小车每隔0.1s离传感器的距离,测
得的数据如下表,(距离单位为cm)
| S1 | S2 | S3 | S4 | S5 |
| 29.94 | 20.80 | 13.22 | 7.24 | 2.84 |
v0=
1.00
1.00
m/s,及每隔0.1s的瞬时速度分别为v1=0.84
0.84
m/s,v2=0.68
0.68
m/s,v3=0.52
0.52
m/s,v4=0.36
0.36
m/s.(2)在图2的坐标上作出v-t图线,并求出小车运动的加速度α=
-1.59
-1.59
m/s2.分析:(1)根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上1、2、3、4点时小车的瞬时速度大小.
(2)用描点法画出小车的瞬时速度随时间变化的关系图线.由v-t图象解加速度的方法是求斜率.
(2)用描点法画出小车的瞬时速度随时间变化的关系图线.由v-t图象解加速度的方法是求斜率.
解答:解;(1)根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,得:
v1=
=0.84m/s
v2=
=0.68m/s
v3=
=0.52m/s
根据匀变速直线运动的推论公式△x=aT2得:
加速度大小a=
=1.59m/s2
.根据运动学公式得:v0=v1+aT=1.00m/s
v4=v3-aT=0.36m/s
(2)用描点法画出小车的瞬时速度随时间变化的关系图线
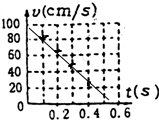
根据v-t图象求出图形的斜率k,
所以小车加速度a=
=-1.59m/s2.
故答案为:(1)1.00,0.84,0.68,0.52,0.36
(2)如图,-1.59
v1=
| S1-S3 |
| 2T |
v2=
| S2-S4 |
| 2T |
v3=
| S3-S5 |
| 2T |
根据匀变速直线运动的推论公式△x=aT2得:
加速度大小a=
| (S1-S3)-(S3-S5) |
| (2T)2 |
.根据运动学公式得:v0=v1+aT=1.00m/s
v4=v3-aT=0.36m/s
(2)用描点法画出小车的瞬时速度随时间变化的关系图线

根据v-t图象求出图形的斜率k,
所以小车加速度a=
| △v |
| △t |
故答案为:(1)1.00,0.84,0.68,0.52,0.36
(2)如图,-1.59
点评:利用匀变速直线的规律以及推论解答实验问题的能力,在平时练习中要加强基础知识的理解与应用,提高解决问题能力.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 小车以某一初速沿水平长木板向左作匀减速运动,长木板左端外有一传感器,通过数据采集器和计算机相连,可测得小车在t时刻离传感器的距离S(如图).现测得小车在初始时刻离传感器的距离为S1,以后每隔0.1s离传感器的距离分别为S2、S3、S4、S5,测得的数据如下表,(距离单位为cm)根据表格中所测得的数据,求:(结果一律取3位有效数字)
小车以某一初速沿水平长木板向左作匀减速运动,长木板左端外有一传感器,通过数据采集器和计算机相连,可测得小车在t时刻离传感器的距离S(如图).现测得小车在初始时刻离传感器的距离为S1,以后每隔0.1s离传感器的距离分别为S2、S3、S4、S5,测得的数据如下表,(距离单位为cm)根据表格中所测得的数据,求:(结果一律取3位有效数字)
| S1 | S2 | S3 | S4 | S5 |
| 29.94 | 20.80 | 13.22 | 7.21 | 2.78 |
(2)小车运动的加速度大小a=______m/s2.
 小车以某一初速沿水平长木板向左作匀减速运动,
小车以某一初速沿水平长木板向左作匀减速运动,
长木板左端外有一传感器,通过数据采集器和计算
机相连,可测得小车每隔0.1s离传感器的距离,测
得的数据如下表,(距离单位为cm)
| S1 | S2 | S3 | S4 | S5 |
| 29.94 | 20.80 | 13.22 | 7.24 | 2.84 |
v0=______m/s,及每隔0.1s的瞬时速度分别为v1=______m/s,v2=______m/s,v3=______m/s,v4=______m/s.
(2)在图2的坐标上作出v-t图线,并求出小车运动的加速度α=______m/s2.
小车以某一初速沿水平长木板向左作匀减速运动,长木板左端外有一传感器,通过数据采集器和计算机相连,可测得小车在t时刻离传感器的距离S(如图).现测得小车在初始时刻离传感器的距离为S1,以后每隔0.1s离传感器的距离分别为S2、S3、S4、S5,测得的数据如下表,(距离单位为cm)根据表格中所测得的数据,求:(结果一律取3位有效数字)
(1)小车离传感器为S3时小车的瞬时速度v3=______m/s;
(2)小车运动的加速度大小a=______m/s2.

| S1 | S2 | S3 | S4 | S5 |
| 29.94 | 20.80 | 13.22 | 7.21 | 2.78 |
(2)小车运动的加速度大小a=______m/s2.

 小车以某一初速沿水平长木板向左作匀减速运动,长木板左端外有一传感器,通过数据采集器和计算机相连,可测得小车在t时刻离传感器的距离S(如图).现测得小车在初始时刻离传感器的距离为S1,以后每隔0.1s离传感器的距离分别为S2、S3、S4、S5,测得的数据如下表,(距离单位为cm)根据表格中所测得的数据,求:(结果一律取3位有效数字)
小车以某一初速沿水平长木板向左作匀减速运动,长木板左端外有一传感器,通过数据采集器和计算机相连,可测得小车在t时刻离传感器的距离S(如图).现测得小车在初始时刻离传感器的距离为S1,以后每隔0.1s离传感器的距离分别为S2、S3、S4、S5,测得的数据如下表,(距离单位为cm)根据表格中所测得的数据,求:(结果一律取3位有效数字)