题目内容
航天员乘坐宇宙飞船探测某行星,飞临该行星后绕行星圆周运动测得行星的密度为ρ.然后降落在该行星表面,在一定高度以初速度v平抛一物体,物体落在行星表面的时间为t,而航天员测得从平抛始点到落点的位移为L.已知万有引力常量为G,该行星表面没有大气,请你根据以上信息计算该行星的第一宇宙速度v1.
根据平抛运动,水平方向做匀速直线运动,而竖直方向做初速度为零的匀加速直线运动,
根据运动学公式,结合牛顿第二定律与几何关系,则有:
=
gt2;
由万有引力等于重力,则有:G
=mg;
且M=ρV=ρ?
πR3;
再根据该行星的第一宇宙速度v1=
;
以上综合,解得:v1=
=
;
答:该行星的第一宇宙速度=
.
根据运动学公式,结合牛顿第二定律与几何关系,则有:
| L2-(vt)2 |
| 1 |
| 2 |
由万有引力等于重力,则有:G
| mM |
| R2 |
且M=ρV=ρ?
| 4 |
| 3 |
再根据该行星的第一宇宙速度v1=
| gR |
以上综合,解得:v1=
|
|
答:该行星的第一宇宙速度=
|

练习册系列答案
相关题目
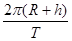
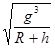
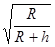
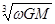
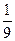 ,则该星球表面附近运行的人造卫星的第一宇宙速度为_____________(用题给已知量表示).
,则该星球表面附近运行的人造卫星的第一宇宙速度为_____________(用题给已知量表示).
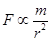 ,行星对太阳的引力
,行星对太阳的引力 ,其中M、m、r分别为太阳、行星质量和太阳与行星间的距离。下列说法正确的是
,其中M、m、r分别为太阳、行星质量和太阳与行星间的距离。下列说法正确的是
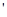 大小相等,是作用力与反作用力
大小相等,是作用力与反作用力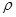 ;石油密度远小于
;石油密度远小于
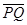 =x,利用“割补法”原理:如果将近地表的球形空腔填满密度为
=x,利用“割补法”原理:如果将近地表的球形空腔填满密度为 来计算,式中M是填充岩石后球形区域的质量,求空腔所引起的Q点处的重力加速度反常值
来计算,式中M是填充岩石后球形区域的质量,求空腔所引起的Q点处的重力加速度反常值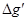 (
(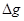 在OP方向上的分量)
在OP方向上的分量)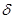 与
与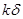 (k>1)(
(k>1)(