题目内容
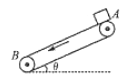
【题目】如图，质量均为 m=1.0 kg 的物块 A、 B 通过轻质弹簧相连，竖放在水平地面上，弹簧的劲度系数 k= 100 N/m。 A、B 的右侧竖立一固定光滑杆 MN，物块 C 穿在竖直杆上。一条不可伸长的轻绳绕过位于 A 正上方的轻质定滑轮 P， --端连接 A，另一端连接 C。开始时物块 C 与轻滑轮 P 等高且 PC 间距 L= 0.3m，绳处于伸直状态但无张力。现将 C 由静止释放，已知它恰好能使 B 离开地面但不继续上升。 (取 g=l0m/s2)
(1)求 C 的质量 mc。
(2)若将 C 换成质量为 1.0 kg 的 D，仍从上述初始位置由静止释放，则 B 离开地面时 D 的速度是多大？
【答案】（1）0.5kg（2）
【解析】（1）开始时对A受力分析可得：kx1=mg（弹簧压缩），x1=0.1m
最终恰好能使B离开地面但不继续上升，说明B此时与地面之间无弹力，且整个系统处于静止状态，对B受力分析可得：kx2=mg（弹簧伸长），x2=0.1m
此时可判断出此时PC间绳子的长度为L′=L+x1+x2=0.5m
则C下降的高度为
因为始末两个状态弹簧的形变量一样，因此弹性势能不变，由能量守恒定律可得： 
解得mC=0.5kg
（2）将C换成D后，由能量守恒可得： 
由几何关系可知： 
解得： 
练习册系列答案
阅读快车系列答案
相关题目
