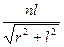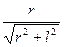题目内容
如图13-1-9所示，一储油圆桶，底面直径与桶高均为d，当桶内无油时，从某点A恰能看到桶底边缘上的某点B，当桶内油的深度等于桶高一半时，在A点沿AB方向看去，看到桶底上的C点，C、B相距
d，由此可得油的折射率n为多少?光在油中传播的速度v为多少?（结果可用根式表示）.
图13-1-9
d，由此可得油的折射率n为多少?光在油中传播的速度v为多少?（结果可用根式表示）.图13-1-9
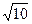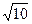/2 6×107作出光路图13-1-10，
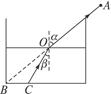
图13-1-10
sinα=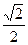
，sinβ=
=
,
而油的折射率n=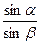
=
，
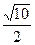光在油中的传播速度v=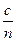
=6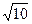×107 m/s.
图13-1-10
sinα=
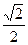，sinβ==,而油的折射率n=
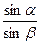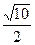=，光在油中的传播速度v=
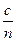=6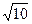×107 m/s.
练习册系列答案
相关题目
。（1）求两条光线经柱面和地面折射后的交点与O点的距离d。（2）若入射的是单色蓝光，则距离d将比上问中求得的结果大还是小？
60°，已知光在真空的速度c=3×108m／s，玻璃的折射率n=1．5。求：
