题目内容
(2007?连云港三模)如图甲所示,质量分别为m=1kg,M=2kg的A、B两个小物块用经弹簧相连而静止在光滑水平面上,在A的左侧某处另有一个质量也为m=1kg的小物块C以v0=4m/s的速度正对A向右匀速运动,一旦与A接触就将粘合在一起运动,若在C与A接触前对A施加一个水平向右的瞬时冲量I,从A获得瞬时冲量作用的时刻开始计时,向右为正方向,其速度随时间变化的图象如图乙所示(C与A未接触前),弹簧始终未超过弹簧性限度.

(1)求对A施加的瞬时冲量I的大小;
(2)在C与A接触前,当A的速度分别为6m/s、2m/s、-2m/s时,求对应状态下B的速度,并在此基础上在图乙中粗略画出B的速度随时间变化图象;
(3)若C分别在A的速度为vA1=4m/s、vA2=-2m/s时与A接触,试计算这两种情况下在接触后的运动过程中弹性势能的最大值Epm1和Epm2.
(4)若C在A的速度为vA时与A接触,在接触后的运动过程中弹性势能的最大值为Epm,试证明Epm与第(3)问中的Epm1、Epm2间满足:Epm1≥Epm≥Epm2.

(1)求对A施加的瞬时冲量I的大小;
(2)在C与A接触前,当A的速度分别为6m/s、2m/s、-2m/s时,求对应状态下B的速度,并在此基础上在图乙中粗略画出B的速度随时间变化图象;
(3)若C分别在A的速度为vA1=4m/s、vA2=-2m/s时与A接触,试计算这两种情况下在接触后的运动过程中弹性势能的最大值Epm1和Epm2.
(4)若C在A的速度为vA时与A接触,在接触后的运动过程中弹性势能的最大值为Epm,试证明Epm与第(3)问中的Epm1、Epm2间满足:Epm1≥Epm≥Epm2.
分析:C与A接触前,A、B组成的系统动量守恒,由动量守恒定律得到B速度的表达式,再代入数据求出B的速度,画出图象.
无论C与A如何接触,当A、B、C具有相同速度u时弹性势能最大.根据系统的动量守恒求出u.再研究A、B碰撞过程,根据动量守恒和能量守恒求出碰撞损失的机械能.由三个物体的系统机械能守恒得到弹簧弹性势能的表达式Ep表达式,分析得到范围.
无论C与A如何接触,当A、B、C具有相同速度u时弹性势能最大.根据系统的动量守恒求出u.再研究A、B碰撞过程,根据动量守恒和能量守恒求出碰撞损失的机械能.由三个物体的系统机械能守恒得到弹簧弹性势能的表达式Ep表达式,分析得到范围.
解答:解:(1)由图可知:对A施加瞬时冲量后的初速度为vA0=6m/s,
所以施加的瞬时冲量I的大小I=mvA0=6N?s
(2)由动量守恒定律 mVA0=mVA+MVB ①
得 vB=
(VA0-VA)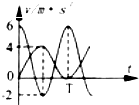
代入数据得 B与A对应的速度为0,2m/s,4m/s
描绘图象如图示
(3)无论C与A如何接触,当A、B、C具有相同速度u时弹性势能最大,
由动量守恒定律 mV0+mVA0=(2m+M)u ②
u=2.5m/s
设C与A碰撞前后A的瞬时速度分别为VA、V,碰撞过程缺失机械能为△E,则
mV0+mVA=2mV ③
△E=
+
-
×2mV2 ④
设最大的弹性势能为Ep,则 Ep=
+
-
(2m+M)u2-△E ⑤
联立②~⑤解得 EP=
+
-
(2m+M)u2-
m(V0-VA)2 ⑥
可见VA=V0时,C与A接触而粘在一起,不损失机械能,△E=0,EP有最大值EPm.代入⑥式得
Epm=
×1×42+
×1×62-
×(2×1+2)×2.52-0=13.5J
当VA反向最大时,△E最大,EP有最小值EPmin.
由第(1)问知,当VA=-2m/s时,B的速度VB=4m/s,这时A、B的总动能 EKAB=
+
=18J
A刚开始运动时,A、B和弹簧组成系统的总能量 EK=
=18J
可见C与A碰撞前,A的反向最大速度不会超过2m/s,代入⑥得
EPm=
×1×42+
×1×62-
×(2×1+2)×2.52-
×2×(4+2)2=4.5J
所以A的速度为vA1=4m/s时与A接触,弹簧弹性势能最大值Epm1=13.5J
A的速度为vA2=-2m/s时与A接触,弹簧弹性势能最大值Epm2=4.5J.
所以弹簧弹性势能最大值的变化范围是 13.5J≥EP≥4.5J
答:(1)对A施加的瞬时冲量I的大小是6N?s;
(2)在C与A接触前,当A的速度分别为6m/s、2m/s、-2m/s时,B与A对应的速度为0,2m/s,4m/s;
(3)若C分别在A的速度为vA1=4m/s、vA2=-2m/s时与A接触,这两种情况下在接触后的运动过程中弹性势能的最大值Epm1=13.5J
Epm2=4.5J.
(4)证明如上.
所以施加的瞬时冲量I的大小I=mvA0=6N?s
(2)由动量守恒定律 mVA0=mVA+MVB ①
得 vB=
| m |
| M |

代入数据得 B与A对应的速度为0,2m/s,4m/s
描绘图象如图示
(3)无论C与A如何接触,当A、B、C具有相同速度u时弹性势能最大,
由动量守恒定律 mV0+mVA0=(2m+M)u ②
u=2.5m/s
设C与A碰撞前后A的瞬时速度分别为VA、V,碰撞过程缺失机械能为△E,则
mV0+mVA=2mV ③
△E=
| 1 |
| 2 |
| mv | 2 0 |
| 1 |
| 2 |
| mv | 2 A |
| 1 |
| 2 |
设最大的弹性势能为Ep,则 Ep=
| 1 |
| 2 |
| mv | 2 0 |
| 1 |
| 2 |
| mv | 2 A0 |
| 1 |
| 2 |
联立②~⑤解得 EP=
| 1 |
| 2 |
| mv | 2 0 |
| 1 |
| 2 |
| mv | 2 A0 |
| 1 |
| 2 |
| 1 |
| 4 |
可见VA=V0时,C与A接触而粘在一起,不损失机械能,△E=0,EP有最大值EPm.代入⑥式得
Epm=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当VA反向最大时,△E最大,EP有最小值EPmin.
由第(1)问知,当VA=-2m/s时,B的速度VB=4m/s,这时A、B的总动能 EKAB=
| 1 |
| 2 |
| mv | 2 A |
| 1 |
| 2 |
| Mv | 2 B |
A刚开始运动时,A、B和弹簧组成系统的总能量 EK=
| 1 |
| 2 |
| mv | 2 A0 |
可见C与A碰撞前,A的反向最大速度不会超过2m/s,代入⑥得
EPm=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以A的速度为vA1=4m/s时与A接触,弹簧弹性势能最大值Epm1=13.5J
A的速度为vA2=-2m/s时与A接触,弹簧弹性势能最大值Epm2=4.5J.
所以弹簧弹性势能最大值的变化范围是 13.5J≥EP≥4.5J
答:(1)对A施加的瞬时冲量I的大小是6N?s;
(2)在C与A接触前,当A的速度分别为6m/s、2m/s、-2m/s时,B与A对应的速度为0,2m/s,4m/s;
(3)若C分别在A的速度为vA1=4m/s、vA2=-2m/s时与A接触,这两种情况下在接触后的运动过程中弹性势能的最大值Epm1=13.5J
Epm2=4.5J.
(4)证明如上.
点评:对于这类弹簧问题注意用动态思想认真分析物体的运动过程,注意过程中的功能转化关系;解答时注意动量守恒和能量守恒列式分析求解.

练习册系列答案
相关题目
 (2007?连云港三模)某兴趣小组对一辆自制遥控小车的性能进行研究,他们让这辆小车在水平的直轨道上由静止开始运动,并将小车运动的全过程记录下来,通过处理转化为v-t图象,如图所示(除2s~10s时间段内的图象为曲线外,其余时间段图象均为直线).已知小车运动的过程中,2s~14s时间段内小车的功率保持不变,在14s末停止遥控而让小车自由滑行.小车的质量为1kg,可认为在整个过程中小车所受到的阻力大小不变.求:
(2007?连云港三模)某兴趣小组对一辆自制遥控小车的性能进行研究,他们让这辆小车在水平的直轨道上由静止开始运动,并将小车运动的全过程记录下来,通过处理转化为v-t图象,如图所示(除2s~10s时间段内的图象为曲线外,其余时间段图象均为直线).已知小车运动的过程中,2s~14s时间段内小车的功率保持不变,在14s末停止遥控而让小车自由滑行.小车的质量为1kg,可认为在整个过程中小车所受到的阻力大小不变.求: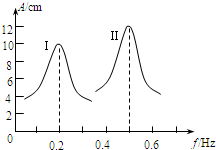 (2007?连云港三模)如图所示为单摆在两次受迫振动中的共振曲线,则下列说法正确的是 ( )
(2007?连云港三模)如图所示为单摆在两次受迫振动中的共振曲线,则下列说法正确的是 ( )