题目内容
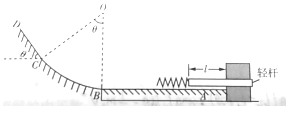
【题目】如图所示，ABCD为固定在竖直平面内的光滑轨道，AB段为水平轨道，BC段为圆心角θ=37°、半径为6l的圆弧轨道，CD段平直倾斜轨道，各段轨道均平滑连接。AB段的右侧有一缓冲装置，劲度系数足够大的轻质弹簧与轻杆相连，轻杆可在固定的槽内移动，轻杆与槽间的滑动摩擦力Ff=4mg，轻杆向右移动不超过l时，装置可安全工作。若将一质量为m的滑块从C点由静止释放，滑块撞击弹簧后将导致轻杆向右移动
。轻杆与槽间的最大静摩擦力等于滑动摩擦力。
（1）若滑块从C点由静止释放，经过圆弧轨道B点时，求滑块对轨道的压力；
（2）为使缓冲装置能安全工作，求允许滑块释放点离C点的最大距离；
（3）在缓冲装置安全工作时，试讨论该物块第一次被弹回后上升距B点的最大高度h'与释放时距B点的高度h之间的关系。
【答案】(1) 
；(2)
； (3)当
，
；当
，
【解析】
(1)从C到B的过程中，机械能守恒
根据牛顿二定律
解得
根据牛顿第三定律，滑块对轨道的压力
(2) 小球从C点由静止释放，推动轻杆后，最终小球剩余的动能变成弹性势能
整理得
设滑块释放点离C点的最大距离为x，根据能量守恒定律
整理得
(3) 如果轻杆没被推动，则小球滑到弹簧处的动能最大值为
，根据机械能守恒
整理得，小球下降的最大高度
当释放点的高度
轻杆不动，弹回上升的最大高度
而当释放点的高度
轻杆被推动，弹回上升的最大高度
练习册系列答案
相关题目
