题目内容
6. 如图所示,质量为m,长为L的均匀木杆AB,A端装有水平转轴,若在B端用恒定的水平外力F使杆从竖直位置绕A转过θ角,则此时木杆的动能为FLsinθ-$\frac{1}{2}$mgL(1-cosθ);在水平恒力F=$\frac{mg}{2}$作用下木杆转过的最大角度为90°.
如图所示,质量为m,长为L的均匀木杆AB,A端装有水平转轴,若在B端用恒定的水平外力F使杆从竖直位置绕A转过θ角,则此时木杆的动能为FLsinθ-$\frac{1}{2}$mgL(1-cosθ);在水平恒力F=$\frac{mg}{2}$作用下木杆转过的最大角度为90°.
分析 根据恒力做功公式W=FScosθ求解F做的功,根据动能定理求解木杆的动能.对整个过程,运用动能定理求木杆转过的最大角度.
解答 解:根据恒力做功公式W=FScosθ,使杆从竖直位置绕A转过θ角的过程中水平外力做功为:WF=FLsinθ
整个过程运用动能定理得木杆的动能为:EK=WF+WG=FLsinθ-$\frac{1}{2}$mgL(1-cosθ)
设木杆转过的最大角度为α.根据动能定理得:FLsinα-$\frac{1}{2}$mgL(1-cosα)=0
将F=$\frac{mg}{2}$代入解得:α=90°
故答案为:$FLsinθ-\frac{1}{2}mgL(1-cosθ)$,90°.
点评 解答本题的关键要掌握恒力做功的求法,求重力做功时由于杆不能看成质点,必须考虑重心上升的高度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.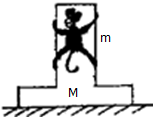 如图所示,滑杆和底座静止在水平地面上,质量为M,一质量为m的猴子沿杆以0.4g的加速度加速下滑,则底座对地面的压力为( )
如图所示,滑杆和底座静止在水平地面上,质量为M,一质量为m的猴子沿杆以0.4g的加速度加速下滑,则底座对地面的压力为( )
 如图所示,滑杆和底座静止在水平地面上,质量为M,一质量为m的猴子沿杆以0.4g的加速度加速下滑,则底座对地面的压力为( )
如图所示,滑杆和底座静止在水平地面上,质量为M,一质量为m的猴子沿杆以0.4g的加速度加速下滑,则底座对地面的压力为( )| A. | Mg+0.4mg | B. | Mg+0.6mg | C. | (M+m)g | D. | Mg |
14.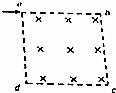 如图所示,在正方形区域abcd中,有方向垂直纸面向里,磁感应强度为B的匀强磁场,一束质量为m、电量为e的电子沿ab边以不同的速率射入磁场,则电子通过磁场的最长时间为( )
如图所示,在正方形区域abcd中,有方向垂直纸面向里,磁感应强度为B的匀强磁场,一束质量为m、电量为e的电子沿ab边以不同的速率射入磁场,则电子通过磁场的最长时间为( )
 如图所示,在正方形区域abcd中,有方向垂直纸面向里,磁感应强度为B的匀强磁场,一束质量为m、电量为e的电子沿ab边以不同的速率射入磁场,则电子通过磁场的最长时间为( )
如图所示,在正方形区域abcd中,有方向垂直纸面向里,磁感应强度为B的匀强磁场,一束质量为m、电量为e的电子沿ab边以不同的速率射入磁场,则电子通过磁场的最长时间为( )| A. | $\frac{πm}{eB}$ | B. | $\frac{2πm}{eB}$ | C. | $\frac{3πm}{eB}$ | D. | $\frac{πm}{2eB}$ |
1.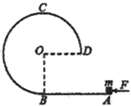 如图所示,在竖直平面内有一固定轨道,其中AB是长为2R的粗糙水平直轨道,BCD是圆心为O、半径为R的$\frac{3}{4}$光滑圆弧轨道,两轨道相切于B点,在推力作用下,质量为m的小滑块从A点由静止开始做匀加速直线运动,到达B点时即撤去推力,小滑块恰好能沿圆轨道经过最高点C重力加速度大小为g,选地面为零势面,则小滑块( )
如图所示,在竖直平面内有一固定轨道,其中AB是长为2R的粗糙水平直轨道,BCD是圆心为O、半径为R的$\frac{3}{4}$光滑圆弧轨道,两轨道相切于B点,在推力作用下,质量为m的小滑块从A点由静止开始做匀加速直线运动,到达B点时即撤去推力,小滑块恰好能沿圆轨道经过最高点C重力加速度大小为g,选地面为零势面,则小滑块( )
 如图所示,在竖直平面内有一固定轨道,其中AB是长为2R的粗糙水平直轨道,BCD是圆心为O、半径为R的$\frac{3}{4}$光滑圆弧轨道,两轨道相切于B点,在推力作用下,质量为m的小滑块从A点由静止开始做匀加速直线运动,到达B点时即撤去推力,小滑块恰好能沿圆轨道经过最高点C重力加速度大小为g,选地面为零势面,则小滑块( )
如图所示,在竖直平面内有一固定轨道,其中AB是长为2R的粗糙水平直轨道,BCD是圆心为O、半径为R的$\frac{3}{4}$光滑圆弧轨道,两轨道相切于B点,在推力作用下,质量为m的小滑块从A点由静止开始做匀加速直线运动,到达B点时即撤去推力,小滑块恰好能沿圆轨道经过最高点C重力加速度大小为g,选地面为零势面,则小滑块( )| A. | 在AB段运动的加速度为1.25g | |
| B. | 到C点时速度为零 | |
| C. | 在C点时重力的瞬时功率为mg$\sqrt{gR}$ | |
| D. | 沿圆轨道上滑时动能与重力势能相等的位置在OD上方 |
11.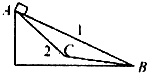 如图所示,物块第一次沿轨道1从A点由静止下滑至底端B点,第二次沿轨道2从A 点由静止下滑经C点至底端B点,AC=CB.物块与两轨道的动摩擦因数相同,不考虑物块在C点处能量损失,则在物块沿两轨道下滑至B点时的速率,判断正确的是( )
如图所示,物块第一次沿轨道1从A点由静止下滑至底端B点,第二次沿轨道2从A 点由静止下滑经C点至底端B点,AC=CB.物块与两轨道的动摩擦因数相同,不考虑物块在C点处能量损失,则在物块沿两轨道下滑至B点时的速率,判断正确的是( )
 如图所示,物块第一次沿轨道1从A点由静止下滑至底端B点,第二次沿轨道2从A 点由静止下滑经C点至底端B点,AC=CB.物块与两轨道的动摩擦因数相同,不考虑物块在C点处能量损失,则在物块沿两轨道下滑至B点时的速率,判断正确的是( )
如图所示,物块第一次沿轨道1从A点由静止下滑至底端B点,第二次沿轨道2从A 点由静止下滑经C点至底端B点,AC=CB.物块与两轨道的动摩擦因数相同,不考虑物块在C点处能量损失,则在物块沿两轨道下滑至B点时的速率,判断正确的是( )| A. | 物块沿1轨道滑至B点时的速率大 | B. | 物块沿2轨道滑至B点时的速率大 | ||
| C. | 物块两次滑至B点时速率相等 | D. | 无法判断 |
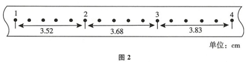
16.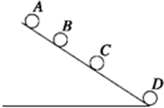 从斜面上某一位置,每隔0.1s释放一个小球,在连续释放几颗小球后,对在斜面上滚动的小球拍下照片,如图所示,测得xAB=20cm,xBC=25cm,则下列说法正确的是( )
从斜面上某一位置,每隔0.1s释放一个小球,在连续释放几颗小球后,对在斜面上滚动的小球拍下照片,如图所示,测得xAB=20cm,xBC=25cm,则下列说法正确的是( )
 从斜面上某一位置,每隔0.1s释放一个小球,在连续释放几颗小球后,对在斜面上滚动的小球拍下照片,如图所示,测得xAB=20cm,xBC=25cm,则下列说法正确的是( )
从斜面上某一位置,每隔0.1s释放一个小球,在连续释放几颗小球后,对在斜面上滚动的小球拍下照片,如图所示,测得xAB=20cm,xBC=25cm,则下列说法正确的是( )| A. | 小球的加速度为5m/s2 | B. | 拍摄时B球的速度为4.5m/s | ||
| C. | 拍摄时xCD的大小为0.3m | D. | A球上方滚动的小球还有2颗 |
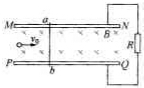 如图所示,MN、PQ为水平放置且足够长的平行金属板,两板间有磁感应强度为B的匀强磁场,磁场的方向垂直纸面向里.轻质金属杆ab的电阻为r,有效长度为l,可以在金属板上左右无摩擦地滑动.与金属板连接的电阻阻值为R.有一带正电荷的粒子以速度v0沿水平方向飞入两板之间,速度方向与磁场方向垂直,不考虑粒子的重力.
如图所示,MN、PQ为水平放置且足够长的平行金属板,两板间有磁感应强度为B的匀强磁场,磁场的方向垂直纸面向里.轻质金属杆ab的电阻为r,有效长度为l,可以在金属板上左右无摩擦地滑动.与金属板连接的电阻阻值为R.有一带正电荷的粒子以速度v0沿水平方向飞入两板之间,速度方向与磁场方向垂直,不考虑粒子的重力.
 如图所示,一重力G1=10N的球A夹在竖直墙与三角劈B的斜面之间,恰能都静止,三角劈的重力G2=20N,劈的斜面倾角θ=37°,劈的斜面与竖直墙面是光滑的,设劈的最大静摩擦力等于滑动摩擦力.sin37°=0.6,cos37°=0.8,求:
如图所示,一重力G1=10N的球A夹在竖直墙与三角劈B的斜面之间,恰能都静止,三角劈的重力G2=20N,劈的斜面倾角θ=37°,劈的斜面与竖直墙面是光滑的,设劈的最大静摩擦力等于滑动摩擦力.sin37°=0.6,cos37°=0.8,求: