题目内容
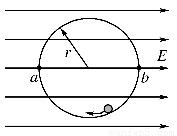
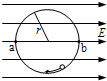 如图,匀强电场中有一半径为r的光滑绝缘圆轨道,轨道平面与电场方向平行.a、b为轨道直径的两端,该直径与电场方向平行.一电荷量为q(q>0)的质点沿轨道内侧运动,经过a点和b点时对轨道压力的大小分别为Na和Nb.不计重力,求电场强度的大小E、质点经过a点和b点时的动能.
如图,匀强电场中有一半径为r的光滑绝缘圆轨道,轨道平面与电场方向平行.a、b为轨道直径的两端,该直径与电场方向平行.一电荷量为q(q>0)的质点沿轨道内侧运动,经过a点和b点时对轨道压力的大小分别为Na和Nb.不计重力,求电场强度的大小E、质点经过a点和b点时的动能.分析:根据牛顿第二定律,将电场力与支持力提供向心力列出方程,并由动能定理来联立求解.
解答:解:质点所受到电场力的大小为:f=qE,
设质点质量为m,经过a点和b点时速度大小分别为va vb,
由牛顿第二定律有,f+Na=m
Nb-f=m
设质点经过a点和b点时动能分别为 Eka 和 Ekb,
则有 Eka=
m
,Ekb=
m
根据动能定理有,Ekb-Eka=2rf
联立解得:E=
(Nb-Na)
Ea=
(Nb+5Na)
Eb=
(5Nb+Na)
答:电场强度的大小:E=
(Nb-Na)、质点经过a点:Ea=
(Nb+5Na) 和b点时的动能:Eb=
(5Nb+Na).
设质点质量为m,经过a点和b点时速度大小分别为va vb,
由牛顿第二定律有,f+Na=m
| ||
| r |
Nb-f=m
| ||
| r |
设质点经过a点和b点时动能分别为 Eka 和 Ekb,
则有 Eka=
| 1 |
| 2 |
| v | 2 a |
| 1 |
| 2 |
| v | 2 b |
根据动能定理有,Ekb-Eka=2rf
联立解得:E=
| 1 |
| 6q |
Ea=
| r |
| 12 |
Eb=
| r |
| 12 |
答:电场强度的大小:E=
| 1 |
| 6q |
| r |
| 12 |
| r |
| 12 |
点评:考查牛顿第二定律、动能定理、向心力公式、电场力的表达式等规律的理解与应用,注意动能定理列式过程中的功的正负.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
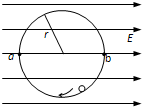 如图,匀强电场中有一半径为r的光滑绝缘圆轨道,轨道平面与电场方向平行.a、b为轨道直径的两端,该直径与电场方向平行.一电荷量为q(q>0)的质点沿轨道内侧运动,经过a点和b点时对轨道压力的大小分别为Na和Nb.不计重力,求:(1)电场强度的大小E;
如图,匀强电场中有一半径为r的光滑绝缘圆轨道,轨道平面与电场方向平行.a、b为轨道直径的两端,该直径与电场方向平行.一电荷量为q(q>0)的质点沿轨道内侧运动,经过a点和b点时对轨道压力的大小分别为Na和Nb.不计重力,求:(1)电场强度的大小E;