题目内容
 (2006?南通一模)如图所示,现有一质量为m、电荷量为e的电子从y轴上的P(0,a)点以初速度v0平行于x轴射出,为了使电子能够经过x轴上的Q(b,0)点,可在y轴右侧加一垂直于x0y平面向里、宽度为L的匀强磁场,磁感应强度大小为B,该磁场左、右边界与y轴平行,上、下足够宽(图中未画出).已知
(2006?南通一模)如图所示,现有一质量为m、电荷量为e的电子从y轴上的P(0,a)点以初速度v0平行于x轴射出,为了使电子能够经过x轴上的Q(b,0)点,可在y轴右侧加一垂直于x0y平面向里、宽度为L的匀强磁场,磁感应强度大小为B,该磁场左、右边界与y轴平行,上、下足够宽(图中未画出).已知| mv0 |
| eB |
| 2mv0 |
| eB |
分析:先根据洛伦兹力提供向心力求解出轨道半径表达式;当r>L时,画出运动轨迹,根据几何关系列式求解;当r≤L时,再次画出轨迹,并根据几何关系列式求解.
解答: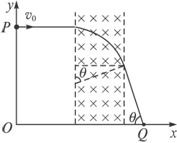 解:设电子在磁场中做圆周运动的轨道半径为r,则eBv0=m
解:设电子在磁场中做圆周运动的轨道半径为r,则eBv0=m
…①
解得r=
…②
(1)当r>L时,磁场区域及电子运动轨迹如下图所示,由几何关系有sinθ=
=
…③
则磁场左边界距坐标原点的距离为
x1=b-L-a-r(1-cosθ)]cotθ…④
x1=b-L-a-
(1-cosθ)]cotθ(其中θ=arcsin
)…⑤
 (2)当r≤L时,磁场区域及电子运动轨迹如下图所示,由几何关系得磁场左边界距坐标原点的距离为
(2)当r≤L时,磁场区域及电子运动轨迹如下图所示,由几何关系得磁场左边界距坐标原点的距离为
x2=b-
…⑥
解得x2=b-
.
答:磁场的左边界距y轴的可能距离为b-L-a-
(1-cosθ)]cotθ(其中θ=arcsin
);也可能为b-
.
 解:设电子在磁场中做圆周运动的轨道半径为r,则eBv0=m
解:设电子在磁场中做圆周运动的轨道半径为r,则eBv0=m
| ||
| r |
解得r=
| mv0 |
| eB |
(1)当r>L时,磁场区域及电子运动轨迹如下图所示,由几何关系有sinθ=
| L |
| r |
| eBL |
| mv0 |
则磁场左边界距坐标原点的距离为
x1=b-L-a-r(1-cosθ)]cotθ…④
x1=b-L-a-
| mv0 |
| eB |
| eBL |
| mv0 |
 (2)当r≤L时,磁场区域及电子运动轨迹如下图所示,由几何关系得磁场左边界距坐标原点的距离为
(2)当r≤L时,磁场区域及电子运动轨迹如下图所示,由几何关系得磁场左边界距坐标原点的距离为x2=b-
| r2-(a-r)2 |
解得x2=b-
|
答:磁场的左边界距y轴的可能距离为b-L-a-
| mv0 |
| eB |
| eBL |
| mv0 |
|
点评:本题关键分r>L和r≤L两种情况讨论,画出轨迹是关键,根据几何关系列方程求解是难点.

练习册系列答案
相关题目
 (2006?南通一模)如图所示,ABC是由折射率为
(2006?南通一模)如图所示,ABC是由折射率为 (2006?南通一模)如图所示,A、B两颗质量相同的人造地球卫星分别在半径不同的轨道上绕地球作匀速圆周运动,则( )
(2006?南通一模)如图所示,A、B两颗质量相同的人造地球卫星分别在半径不同的轨道上绕地球作匀速圆周运动,则( ) (2006?南通一模)某同学采用如图所示的装置来研究光电效应现象.某单色光照射光电管的阴极K时,会发生光电效应现象.闭合开关S,在阳极A和阴极K之间加反向电压,通过调节滑动变阻器的滑片逐渐增大电压,直至电流计中电流恰为零,此时电压表显示的电压值U称为反向截止电压.根据反向截止电压,可以计算出光电子的最大初动能Ekm.现分别用频率为ν1和ν2的单色光照射阴极,测量到的反向截止电压分别为Ul和U2,设电子质量为m,电荷量为e,则下列关系式中不正确的是( )
(2006?南通一模)某同学采用如图所示的装置来研究光电效应现象.某单色光照射光电管的阴极K时,会发生光电效应现象.闭合开关S,在阳极A和阴极K之间加反向电压,通过调节滑动变阻器的滑片逐渐增大电压,直至电流计中电流恰为零,此时电压表显示的电压值U称为反向截止电压.根据反向截止电压,可以计算出光电子的最大初动能Ekm.现分别用频率为ν1和ν2的单色光照射阴极,测量到的反向截止电压分别为Ul和U2,设电子质量为m,电荷量为e,则下列关系式中不正确的是( )