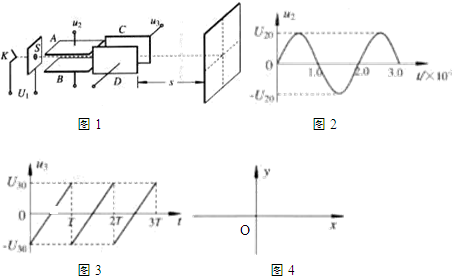
题目内容
如图(1)所示，真空室中电极K发出的电子(初速不计)经过U0＝1000伏的加速电场后，由小孔S沿两水平金属板A、B间的中防线射入，A、B板长l＝0.02米，相距d＝0.020米，加在A、B两板间的电压u随时间t变化u－t图线如图(2)所示，设A、B间的电场可看作是均匀的，且两板外无电场，在每个电子通过电场区域的极短时间内，电场可视作恒定的．两板右侧放一记录圆筒，筒的左侧边缘与极右端距离b＝0.15米，筒绕其竖直轴匀速转动，周期T＝0.20秒，筒的周长s＝0.20米，筒能接收到通过A、B板的全部电子．
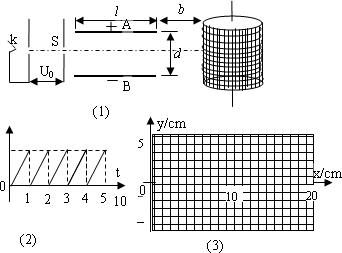
(1)以t＝0时[见图(2)]，此时u＝0，电子打到圆筒记录纸上的点作为xy坐标系的原点，并取y轴竖直向上，试计算电子打到记录纸上的最高点的y坐标和x坐标．(不计重力作用)
(2)在给出的坐标纸图(3)上定量地画出电子打到记录纸上的点形成的图线．
答案：
解析：
解析：
|
(1)计算电子打到记录纸上的最高点的坐标，设v0为电子A、B板的中心线射入电场时的初速度，则 |
，电子在中心线方向的运动为匀速运动，设电子穿过A、B板的时间为t0，则
，电子在垂直A、B板方向的运动为匀加速直线运动，对于恰能穿过A、B板的电子，在它通过时加在两板间的电压UC应满足
，联立上面三式得
，此电子从A、B板射出时沿y方向的分速度为
，以后，此电子做匀速直线运动，它打在记录纸上的点最高．设纵坐标为y．由答图可得，
练习册系列答案
相关题目
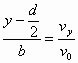
如图1所示，真空中有竖直放置的平行金属板A、B和水平放置相距为d的平行金属板C、D，C、D板长为L，A、B板间加有恒定的电压U0，质量为m、电荷量为q的带电粒子从A板静止释放，经AB间的电场加速后进入C、D两板的正中间．在带电粒子进入C、D间的同时，给C、D两板加上如图2所示周期性变化的交变电压，（粒子重力不计）求：
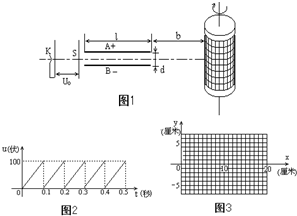如图1所示，真空室中电极K发出的电子（初速不计）经过U0=1000V的加速电场后，由小孔S沿两水平金属板A、B间的中心线射入．A、B板长l=0.20m，相距d=0.020m，加在A、B两板间的电压u随时间t变化的u-t图线如图2所示．设A、B间的电场可看作是均匀的，且两板外无电场．在每个电子通过电场区域的极短时间内，电场可视作恒定的．两板右侧放一记录圆筒，筒在左侧边缘与极板右端距离b=0.15m，筒绕其竖直轴匀速转动，周期T=0.20s，筒的周长s=0.20m，筒能接收到通过A、B板的全部电子．