题目内容
(2006?北京)如图1所示,真空中相距d=5cm的两块平行金属板A、B与电源连接(图中未画出),其中B板接地(电势为零),A板电势变化的规律如图2所示.将一个质量m=2.0×10-27kg,电量q=+1.6×10-19C的带电粒子从紧临B板处释放,不计重力.求
(1)在t=0时刻释放该带电粒子,释放瞬间粒子加速度的大小;
(2)若A板电势变化周期T=1.0×10-5s,在t=0时将带电粒子从紧临B板处无初速释放,粒子达到A板时动量的大小;
(3)A板电势变化频率多大时,在t=
到t=
时间内从紧临B板处无初速释放该带电粒子,粒子不能到达A板.

(1)在t=0时刻释放该带电粒子,释放瞬间粒子加速度的大小;
(2)若A板电势变化周期T=1.0×10-5s,在t=0时将带电粒子从紧临B板处无初速释放,粒子达到A板时动量的大小;
(3)A板电势变化频率多大时,在t=
| T |
| 4 |
| T |
| 2 |

分析:(1)由图可知两板间开始时的电势差,则由U=Ed可求得两板间的电场强度,则可求得电场力,由牛顿第二定律可求得加速度的大小;
(2)因粒子受力可能发生变化,故由位移公式可求得粒子通过的距离,通过比较可知恰好到A板,故电场力不变,由动量定理可求得动量;
(3)要使粒子不能到达A板,应让粒子在向A板运动中的总位移小于极板间的距离,由以上表达式可得出变化的频率.
(2)因粒子受力可能发生变化,故由位移公式可求得粒子通过的距离,通过比较可知恰好到A板,故电场力不变,由动量定理可求得动量;
(3)要使粒子不能到达A板,应让粒子在向A板运动中的总位移小于极板间的距离,由以上表达式可得出变化的频率.
解答:解:(1)电场强度E=
,带电粒子所受电场力F=qE=
,F=ma
a=
=4.0×109m/s2
释放瞬间粒子的加速度为4.0×109m/s2;
(2)粒子在0~
时间内走过的距离为
a(
)2=5.0×10-2m
故带电粒子在t=
时,恰好到达A板,根据动量定理,此时粒子动量p=Ft=4.0×10-23kg?m/s
粒子到达A板时的动量为4.0×10-23kg?m/s
(3)带电粒子在0~t=
向A板做匀加速运动,在t=
~t=
向A板做匀减速运动,速度减为零后将返回.粒子向A 板运动可能的最大位移s=2×
a(
)2=
aT2
要求粒子不能到达A板,有s<d,由f=
,电势变化频率应满足f>
=5
×104Hz
电势变化的频率应满足f>5
×104Hz.
| U |
| d |
| Uq |
| d |
a=
| Uq |
| dm |
释放瞬间粒子的加速度为4.0×109m/s2;
(2)粒子在0~
| T |
| 2 |
| 1 |
| 2 |
| T |
| 2 |
故带电粒子在t=
| T |
| 2 |
粒子到达A板时的动量为4.0×10-23kg?m/s
(3)带电粒子在0~t=
| T |
| 2 |
| T |
| 2 |
| 3T |
| 4 |
| 1 |
| 2 |
| T |
| 4 |
| 1 |
| 16 |
要求粒子不能到达A板,有s<d,由f=
| 1 |
| T |
|
| 2 |
电势变化的频率应满足f>5
| 2 |
点评:因极板间加交变电场,故粒子的受力周周期性变化,本题应通过受力情况先确定粒子的运动情况,再确定两板间电势的变化频率.

练习册系列答案
相关题目
 (2006?北京)木块A、B分别重50N和60N,它们与水平地面之间的动摩擦因数均为0.25.夹在A、B之间的轻弹簧被压缩了2cm,弹簧的劲度系数为400N/m.系统置于水平地面上静止不动.现用F=1N的水平拉力作用在木块B上,如图所示,力F作用后( )
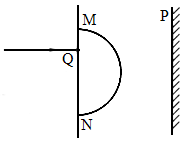
(2006?北京)木块A、B分别重50N和60N,它们与水平地面之间的动摩擦因数均为0.25.夹在A、B之间的轻弹簧被压缩了2cm,弹簧的劲度系数为400N/m.系统置于水平地面上静止不动.现用F=1N的水平拉力作用在木块B上,如图所示,力F作用后( ) (2006?北京)如图所示,均强磁场的方向垂直纸面向里,一带电微粒从磁场边界d点垂直与磁场方向射入,沿曲线dpa打到屏MN上的a点,通过pa段用时为t.若该微粒经过p点时,与一个静止的不带电微粒碰撞并结合为一个新微粒,最终打到屏MN上.两个微粒所受重力均忽略.新微粒运动的( )
(2006?北京)如图所示,均强磁场的方向垂直纸面向里,一带电微粒从磁场边界d点垂直与磁场方向射入,沿曲线dpa打到屏MN上的a点,通过pa段用时为t.若该微粒经过p点时,与一个静止的不带电微粒碰撞并结合为一个新微粒,最终打到屏MN上.两个微粒所受重力均忽略.新微粒运动的( ) (2006?北京)如图是简化后的跳台滑雪的雪道示意图.整个雪道由倾斜的助滑雪道AB和着陆雪道DE,以及水平的起跳平台CD组成,AB与CD圆滑连接.运动员从助滑雪道AB上由静止开始,在重力作用下,滑到D点水平飞出,不计飞行中的空气阻力,经2s在水平方向飞行了60m,落在着陆雪道DE上,已知从B点到D点运动员的速度大小不变.(g取10m/s2)求
(2006?北京)如图是简化后的跳台滑雪的雪道示意图.整个雪道由倾斜的助滑雪道AB和着陆雪道DE,以及水平的起跳平台CD组成,AB与CD圆滑连接.运动员从助滑雪道AB上由静止开始,在重力作用下,滑到D点水平飞出,不计飞行中的空气阻力,经2s在水平方向飞行了60m,落在着陆雪道DE上,已知从B点到D点运动员的速度大小不变.(g取10m/s2)求 .如果保持入射光线和光屏的位置不变,而使半圆形玻璃砖沿直径方向向上或向下移动,移动的距离小于
.如果保持入射光线和光屏的位置不变,而使半圆形玻璃砖沿直径方向向上或向下移动,移动的距离小于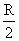 ,则有
,则有