题目内容
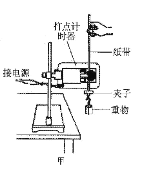
【题目】如图所示,竖直面内的光滑四分之一圆弧轨道AB与光滑的半圆弧轨道BC在B点平滑连接,四分之一圆弧的圆心与C点重合,半圆弧的直径BC沿竖直方向,一个小球在A点正上方某高度处由静止释放,无碰撞地进人轨道,并恰好能到达C点,半圆弧的半径为R,重力加速度为g,求:
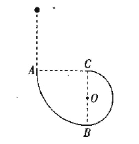
(1)运动到B点前和B点后一瞬间对轨道的压力大小之比;
(2)小球从C点飞出后,第一次落到四分之一圆弧轨道上的位置离B点的高度为多少?
(3)若仅将半圆弧轨道的半径增大为3R,圆心仍在过B点的竖直线上,两圆弧轨道仍在B点平滑连接,要使小球第一次运动到半圆弧轨道上时,不会脱离轨道,则小球下落时的位置离B点的高度应满足什么条件?
【答案】(1)![]() (2)(3-
(2)(3-![]() )R (3)
)R (3)![]()
【解析】
(1)由于小球刚好能到达C点,则
mg=m![]()
从B到C的过程机械能守恒,则有
2mgR=![]()
设小球到达B点前一瞬间轨道对小球的支持力为![]() 到达B点后一瞬间轨道对小球的支持力为
到达B点后一瞬间轨道对小球的支持力为![]() ,则有
,则有
![]()
求得![]() mg
mg
![]()
求得![]() mg
mg
根据牛顿第三定律,小球到达B点后一瞬间对轨道的压力
![]()
小球到达B点后一瞬间对轨道的压力
![]()
因此有![]()
(2)小球从C点飞出做平抛运动,以C点为坐标原点,向下向左建立直角坐标系,设小球第一次落到轨道上的位置坐标为(x,y)
则有
x=![]()
y=![]() gt
gt
x+y=(2R)
求得
y=(![]()
落点离B点的高度
h=2R-y=(3-![]() )R
)R
(3)设小球下落点离B点的高度为![]() 时,小球刚好能运动到半圆弧最高点,设此时在最高点的速度为v,
时,小球刚好能运动到半圆弧最高点,设此时在最高点的速度为v,
则根据牛顿第二定律有
mg=![]()
根据机械能守恒定律有
mg![]() =
=![]() mv+6mgR
mv+6mgR
求得![]()
设小球下落点离B点的高度为![]() ,小球刚好能运动到半圆弧轨道上与圆心等高的位置,根据机械能守恒定律
,小球刚好能运动到半圆弧轨道上与圆心等高的位置,根据机械能守恒定律
mg![]()
可得![]() =3R
=3R
要使小球第一次运动到半圆弧轨道上时,不会脱离轨道,则小球下落时的位置离B点的高度h应满足:![]() 或
或![]()

练习册系列答案
相关题目