Question

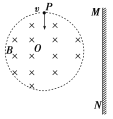
【题目】一个闭合回路由两部分组成，如图所示，右侧水平面上是匝数，电阻为的圆形导线圈，线圈所围面积为，置于竖直向上均匀增强的磁场中，随时间的变化率为；左侧是倾角为的足够长平行金属导轨，宽度为，导轨电阻及与线圈连接的导线电阻均忽略不计。磁感应强度为的匀强磁场垂直导轨平面向下，且只分布在左侧区域，是一个质量为、电阻为的导体棒，棒与导轨垂直且与导轨间动摩擦因数为，将棒由静止释放，取，，。求：

(1)刚释放瞬间，棒中的电流及棒的加速度；

(2)棒最终匀速运动时，速度的大小。

Answer 1

【答案】(1)0.2A ，3m/s2，(2)9.6m/s。

【解析】

(1)根据法拉第电磁感应定律可得线圈中产生的感应电动势为：

回路的电流为：

根据楞次定律可知中的电流方向从到，根据左手定则可知安培力方向沿斜面向下；根据牛顿第二定律可得：

代入数据解得：，方向沿导轨向下；

(2)导体棒匀速运动时受力平衡，安培力方向沿导轨向上，根据平衡条件可得：

解得：

根据闭合电路的欧姆定律可得：

解得：。