题目内容
7.小船在100m宽的河中横渡,水流速度为3m/s,船静水中的速度为5m/s,求:①当小船船头正对河岸时,渡河时间是多少?到达对岸时在何处?
②要使小船到达正对岸,应如何行驶,渡河时间是多少?
分析 ①将小船运动分解为沿河岸方向和垂直于河岸方向,根据垂直于河岸方向上的速度求出渡河的时间,再根据沿河岸方向上的运动求出沿河岸方向上的位移.
②当合速度与河岸垂直时,将运行到正对岸,求出合速度的大小,根据河岸求出渡河的时间.
解答 解:①渡河时间t=$\frac{d}{{v}_{c}}$=$\frac{100}{5}$s=20s.
那么沿着水流方向的位移,x=vst=3×20m=60m.
②当合速度于河岸垂直,小船到达正对岸.
设静水速的方向与河岸的夹角为θ.
cosθ=$\frac{{v}_{s}}{{v}_{c}}$=$\frac{3}{5}$,知θ=53°.
合速度的大小为v=$\sqrt{{v}_{c}^{2}-{v}_{s}^{2}}$=4m/s
则渡河时间t=$\frac{d}{v}$=$\frac{100}{4}$s=25s.
答:①当小船船头正对河岸时,渡河时间是20s,到达对岸时在正对岸下游60m处;
②要使小船到达正对岸,应偏向上游与河岸的夹角为53°行驶,渡河时间是25s.
点评 解决本题的关键知道合运动与分运动具有等时性,当静水速与河岸垂直,渡河时间最短;当合速度与河岸垂直,渡河航程最短.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
15.从A点以9.8m/s的初速度水平抛出一个物体,物体飞行一段时间后以与水平方向成45度角落地,这个物体的飞行时间为( )
| A. | 1 s | B. | $\frac{2}{{\sqrt{3}}}$s | C. | $\sqrt{3}$s | D. | 2s |
16.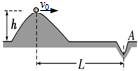 如图所示,某人从高出水平地面h的坡上水平击出一个质量为m的高尔夫球由于受恒定的水平风力的作用,高尔夫球竖直落入距击球点水平距离为L的A穴,不计洞穴的深度,则下列说法正确的是( )
如图所示,某人从高出水平地面h的坡上水平击出一个质量为m的高尔夫球由于受恒定的水平风力的作用,高尔夫球竖直落入距击球点水平距离为L的A穴,不计洞穴的深度,则下列说法正确的是( )
 如图所示,某人从高出水平地面h的坡上水平击出一个质量为m的高尔夫球由于受恒定的水平风力的作用,高尔夫球竖直落入距击球点水平距离为L的A穴,不计洞穴的深度,则下列说法正确的是( )
如图所示,某人从高出水平地面h的坡上水平击出一个质量为m的高尔夫球由于受恒定的水平风力的作用,高尔夫球竖直落入距击球点水平距离为L的A穴,不计洞穴的深度,则下列说法正确的是( )| A. | 球被击出后做平抛运动 | |
| B. | 该球从被击出到落入A穴所用的时间为$\frac{L}{{V}_{0}}$ | |
| C. | 球被击出时的初速度大小为L$\sqrt{\frac{2g}{h}}$ | |
| D. | 球被击出后受到的水平风力的大小为$\frac{mgh}{L}$ |
 某款节能环保汽车启动时的工作电路如图所示,查得电源的电动势E=12V,电源的内阻r及保护电阻R阻值未知,当在第一次S1闭合,S2断开的情况下,电流表的示数为1A;在第二次S1、S2均闭合的情况下,电流表的示数为3A.测得第二次车灯的功率减少了75%,若电动机内阻RM=1Ω,电流表的内阻不计且假定车灯灯丝电阻不变,求S1、S2均闭合时电动机的机械功率.
某款节能环保汽车启动时的工作电路如图所示,查得电源的电动势E=12V,电源的内阻r及保护电阻R阻值未知,当在第一次S1闭合,S2断开的情况下,电流表的示数为1A;在第二次S1、S2均闭合的情况下,电流表的示数为3A.测得第二次车灯的功率减少了75%,若电动机内阻RM=1Ω,电流表的内阻不计且假定车灯灯丝电阻不变,求S1、S2均闭合时电动机的机械功率. 如图所示,S点是波源,振动频率f=100Hz,产生的简谐波向右传播,波速v=80m/s,波在传播过程中经过P、Q两点,已知SP=4.2m,SQ=5.4m.
如图所示,S点是波源,振动频率f=100Hz,产生的简谐波向右传播,波速v=80m/s,波在传播过程中经过P、Q两点,已知SP=4.2m,SQ=5.4m.