题目内容
 如图所示,匀强电场的电场强度为E,一带电小球质量为m,轻质悬线长为l,静止时悬线与竖直方向成30°角.
如图所示,匀强电场的电场强度为E,一带电小球质量为m,轻质悬线长为l,静止时悬线与竖直方向成30°角.(1)小球带何种电荷,电荷量是多少?
(2)剪断细线后,小球的加速度有多大?
(3)剪断细线后,经过时间t小球的位移是多少?
分析:(1)小球处于静止状态,分析受力情况,作出受力图,根据电场力与场强方向的关系判断其电性.
(2)将细线突然剪断小球将沿细线方向做匀加速直线运动,根据牛顿第二定律求解加速度.
(3)根据匀变速直线运动位移公式求解时间t小球的位移.
(2)将细线突然剪断小球将沿细线方向做匀加速直线运动,根据牛顿第二定律求解加速度.
(3)根据匀变速直线运动位移公式求解时间t小球的位移.
解答:解:(1)小球受力如图,由于电场力F与场强方向相反,说明小球带负电.
(2)剪断细线后小球将沿细线方向做初速度为零的匀加速直线运动,
小球所受的合外力 F合=
=
=
mg
根据牛顿第二定律得:F合=ma
解得:a=
=
=
g
(3)剪断细线后,经过时间t小球的位移为:x=
at2=
?
gt2=
gt2.
答:(1)小球带负电荷.
(2)剪断细线后,小球的加速度为
g.
(3)剪断细线后,经过时间t小球的位移是
gt2.

(2)剪断细线后小球将沿细线方向做初速度为零的匀加速直线运动,
小球所受的合外力 F合=
| mg |
| cos30° |
| mg | ||||
|
2
| ||
| 3 |
根据牛顿第二定律得:F合=ma
解得:a=
| F合 |
| m |
| ||||
| m |
2
| ||
| 3 |
(3)剪断细线后,经过时间t小球的位移为:x=
| 1 |
| 2 |
| 1 |
| 2 |
2
| ||
| 3 |
| ||
| 3 |
答:(1)小球带负电荷.
(2)剪断细线后,小球的加速度为
2
| ||
| 3 |
(3)剪断细线后,经过时间t小球的位移是
| ||
| 3 |
点评:本题是带电体在电场中平衡问题,分析受力情况是解题的关键,并能根据受力情况判断小球的运动情况.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
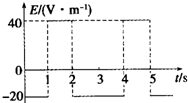 如图所示为匀强电场的电场强度E随时间t变化的图象.当t=0时,在此匀强电场中由静止释放一个带电粒子,设带电粒子只受电场力的作用,则下列说法中正确的是( )
如图所示为匀强电场的电场强度E随时间t变化的图象.当t=0时,在此匀强电场中由静止释放一个带电粒子,设带电粒子只受电场力的作用,则下列说法中正确的是( )| A、带电粒子将始终向同一个方向运动 | B、2s末带电粒子回到原出发点 | C、3s末带电粒子的速度不为零 | D、O~3s内,电场力做的总功为零 |
 如图所示,匀强电场的电场线与AC平行,把带电荷量10-8 C的负电荷从A移至B的过程中,电场力做功6×10-8 J,AB长6cm,AB与AC的夹角为60°.求:
如图所示,匀强电场的电场线与AC平行,把带电荷量10-8 C的负电荷从A移至B的过程中,电场力做功6×10-8 J,AB长6cm,AB与AC的夹角为60°.求: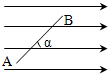 如图所示,匀强电场的场强E=3×105V/m,A、B两点相距0.2m,两点连线与电场的夹角是60°,下列说法正确的是( )
如图所示,匀强电场的场强E=3×105V/m,A、B两点相距0.2m,两点连线与电场的夹角是60°,下列说法正确的是( ) 如图所示,匀强电场的场强E=4.0×104N/C,沿电场线方向有A、B两点,A、B两点间的距离x=0.20m.将电荷量q=+2.0×10-8C的点电荷从A点移至B点.求:
如图所示,匀强电场的场强E=4.0×104N/C,沿电场线方向有A、B两点,A、B两点间的距离x=0.20m.将电荷量q=+2.0×10-8C的点电荷从A点移至B点.求: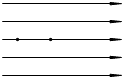 如图所示,匀强电场的电场强度E=2.0×104N/C,沿电场线方向有A、B两点,A、B两点间的距离s=0.10m.将电荷量q=+2.0×10-8C的点电荷从A点移至B点.求:
如图所示,匀强电场的电场强度E=2.0×104N/C,沿电场线方向有A、B两点,A、B两点间的距离s=0.10m.将电荷量q=+2.0×10-8C的点电荷从A点移至B点.求: