Question

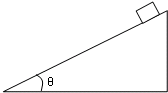一个物体从倾角为θ的斜面顶端由静止开始匀加速滑下，若斜面长为L，物体与斜面间的摩擦系数为μ．求：
1）物体下滑的加速度；
2）物体到达斜面底端时的速度．

Answer 1

分析：根据牛顿第二定律求出物体下滑的加速度，结合速度位移公式求出物体到达底端时的速度．

解答：解：（1）根据牛顿第二定律得，a=

mgsinθ-μmgcosθ

m

=gsinθ-μgcosθ．
（2）根据v²=2aL得，
v=

2aL

=

2(gsinθ-μgcosθ)L

．
答：（1）物体下滑的加速度为gsinθ-μgcosθ．
（2）物体到达斜面底端时的速度为

2(gsinθ-μgcosθ)L

．

点评：本题考查了牛顿第二定律和运动学公式的基本运用，比较简单，知道加速度是联系力学和运动学的桥梁．