��Ŀ����
����Ŀ����ͼ��ʾ����ˮƽ���ҵ���ǿ�糡�У�ˮƽ���AB������һԲ�ι����Բ�ι���̶�����ֱƽ���ڣ�����͵�B��ˮƽ���ƽ�����ӡ�����һ����Ϊm�������Ϊq�Ĵ�����ɵ�С����Ϊ�ʵ㣩������Բ�ι����͵�B���ΪL����C���ɾ�ֹ��ʼ�ڵ糡����������ˮƽ����˶�����֪С�����ܵ糡���������ܵ�������С��ȣ��������ٶ�Ϊg��ˮƽ�����Բ�ι������Ե��С�����˶����������������q���ֲ��䣬����һ��Ħ���Ϳ�����������
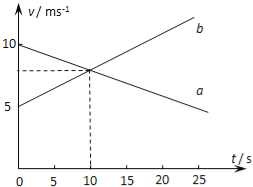
��1����ǿ�糡�ĵ糡ǿ��E�Ĵ�С��
��2��С����C���˶���B�����õ�ʱ��t��
��3��С���˶�����Բ�ι��Բ��O�ȸߵ�D��ʱ���ٶȴ�СvD��

���𰸡���1��mg/q����2��![]() ����3��
����3��![]() ��
��
�������������������1����С��������ɵã�Eq=mg
��ã�E=mg/q
��2����С�����C��B�ļ��ٶ�Ϊa��
����ţ�ٵڶ����ɿɵã�Eq=ma
���˶�ѧ��ʽ�ɵã�![]()
�����ɽ�ã�![]()
��3����Բ�ι���뾶ΪR����С���C��D�Ĺ��̣����ݶ��ܶ����У�
qE��L+R��-mgR=![]() mvD2-0
mvD2-0
�����ڢ����ɵã�vD=![]()

��ϰ��ϵ�д�
 ���100��1�ž�ϵ�д�
���100��1�ž�ϵ�д�
�����Ŀ