题目内容
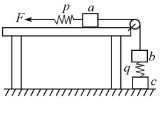
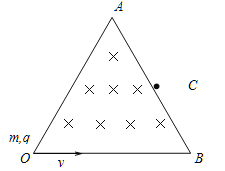
【题目】如图所示,在杆上的下端B点固定一个电量为Q = + 4×10-5C的点电荷。质量为m = 2×10-3kg的小球穿在绝缘细杆上,杆的倾角为α =30o,小球带正电,电量为q=10-8C(小球可看作试探电荷),将小球由距B点竖直高度为H =0.5m的A点处静止释放,小球下滑过程中电量不变。不计小球与细杆间的摩擦,整个装置处在真空中,已知静电力常量k=9.0×109N·m2/C2和重力加速度g=10m/s2,求:
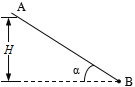
(1)小球刚释放时的加速度大小?
(2)当小球的动能最大时,此时小球与B点的距离?
(3)若小球到达细杆上某点D点(图中未画出)时,小球速度恰好为零,测得点电荷Q形成的电场在A、D两点间的电势差UAD=-6.4×105V,则D点与B点的距离?
【答案】(1)3.2m/s2(2)0.6m(3)0.36m
【解析】
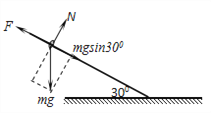
(1)如右图所示,小球刚释放时,受到重力,沿杆向上的库伦力和杆的支持力,由牛顿第二定律可得:
![]()
![]()
a=3.2m/s2
(2)动能最大时:此时小球所受合外力为零,即:a=0
设此时小球与B点距离为L1,由牛顿第二定律可得:
![]()
L1=0.6m
(3)小球运动到D点时,速度恰好为零,设小球下落高度为h,由动能定理可得:
![]()
小球沿杆下滑距离![]()
D点与B点距离![]()
LDB =0.36m

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目